Tabular processor for X-ray diffractometry helps with common calculations in the practice of X-ray structure analysis: calculate the lattice parameters (edges, angles), estimate the quality of results, search the indices of reflections from unknown structures, calculate the reflection grid for known lattice, check the goniometer and specimen alignment.
Program operations are accessible via main menu (use a mouse or F10 key), toolbar buttons or key commands. The context help is available any time by F1 key or Help button in the program dialogs (exception: Open and Save file dialogs may show the Windows help by F1 key, use Help button). To find a specific term or expression in documentation, use the command Ctrl+F in this help window.
The toolbar buttons and key commands allow to perform many operations without opening the main menu. If the screen font is small, screen width decreases and some less important toolbar buttons will be hidden. In such case, use the keys or menu. Description of chosen command is shown in the status line at the bottom of main screen, as well as context information and helpful tips. Some menus can be called by left-click on the corresponding field, like emission, lattice type, cell centring and change indices.
Note: the colours used in this documentation mostly follow the classic colour scheme. For other schemes, the colours and contrast may differ. If you use high contrast themes in Windows, colours in the program and documentation may differ significantly; also the examples, which you can copy to clipboard by left-click, will be marked by dashed border.
Calculated lattice types: from cubic to triclinic. Calculated data: lattice edges, angles, cell volume; c/a relation for hexagonal, tetragonal and orthorhombic lattices; orthorhombic splitting.
Limits by indices h k l : from 0 to 99 Limits by interplanar distances: 0.02...99 Å Limits by lattice edges a, b, c: 2...99 Å Limits by lattice angles : 1...179° Precision of edge calculation : 0.00001 Å Maximum table size : 440 lines Number of labelled phases : 5
All calculations can be performed in ångströms (Å) or in nanometres (nm) as a length unit.
F1 - context help
F3 - open a file (also Ctrl+O)
F4 - select the emission (wavelength)
F5 - set the lattice type (syngony)
F6 - calculate lattice parameters
F7 - set the Bravais cell centring
F8 - clear all or specified data in the table
F9 - print the table (also Ctrl+P)
F10 - enter the main menu
F11 - mark the lines as belonging to a phase
Esc - cancel; stop of auto recalculation
Ctrl+N - new table (clear all current data)
Ctrl+S - write table to current *htm or *.par file
Ctrl+E - write to *htm, *.par, *.txt, *.csv file
Ctrl+R - read one of the recent files
Ctrl+B - copy table and results to clipboard
Alt+N - input the specimen name and its description
Alt+E - input 2θ correction and precision
Alt+F - select the font for main screen
Alt+O - change the configuration of the program
Alt+D - show the chart of deviation and details
of calculation of lattice parameters
Alt+M - calculate density and attenuation length
Alt+P - calculate specimen displacement
Alt+A - calculate cell data and lines with h k l
Alt+G - generate h k l and calculate reflections
Alt+U - calculate texture coefficients
Alt+I - start indexing by shuffle
Alt+B - start indexing by known h k l
Alt+R - show the results of indexing
Alt+K - change the indices of current phase
Alt+X - exit the program (also F12)
Ctrl+Z - undo the last line operation
Ctrl+X - cut current line and copy to clipboard
Ctrl+C - copy current line to clipboard
Ctrl+V - paste data from clipboard to new line
Ctrl+I - insert empty line in current place
Enter - edit data in the current line (also F2)
Space - select or unselect current line
Ins - select phase number or class for current line
Ctrl+L - select the lines of current phase,
unselect other lines
Ctrl+A - select all lines with complete data
Ctrl+T - invert selection of all complete lines
Shift+C - copy selected lines to clipboard
Shift+A - copy all table lines to clipboard
Shift+V - show or edit current content of clipboard
R - sort the lines in specified direction
Shift+R - set the column and direction for sort
Shift+Up,
Shift+Dn - select or unselect a sequence of lines
Shift+Home,
Shift+End - select or unselect the lines from
current line to top or end of the table
Shift+F10,
Context - show context menu for current line
N - assign an ordinal number to a line 1...4 - assign a specified phase, (1)...(4) S - mark a line as standard substance X - exclude a line from calculations B - set a line as basic for indexing
Enter - input value, go to next field or line Esc - restore value in the field, exit edit mode Tab - go to next field Shift+Tab - go to previous field Ctrl+Z - undo the last field edit operation
Home - move marker to begin of the table End - move marker to end of the table PgUp, PgDn - move marker up or down by one page Wheel - scroll the marker first, then table Shift+wheel - scroll the table Ctrl+(Num+) - increase font: zoom in Ctrl+(Num-) - decrease font: zoom out Ctrl+(Num*) - restore default font size Ctrl+wheel - zoom in / zoom out
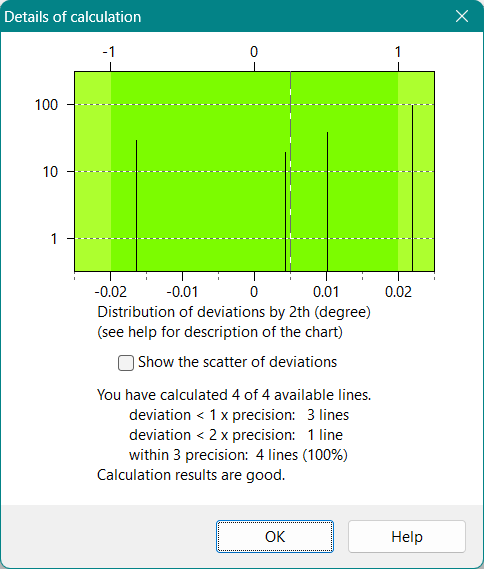
(rms - root mean square, dev - abs. deviation,
prec - precision of 2θ, i.e. ±2th)
excellent: dev < prec for all lines
very well: rms dev < rms prec × 1
well: rms dev < rms prec × 2
satisfactory: rms dev < rms prec × 3
poor: rms dev > rms prec × 3
quality decreases:
by 1, if lines number < parameters number × 2
(for lattices with 3 and more parameters)
by 1, if lines number = parameters number + 1
(for all lattices)
not defined, if lines number = parameters number
This menu includes the operations with the table.
Open - read a data file in available format Clear - clear entire table or particular data Save - write table to current *htm or *.par file Save as - write to *htm, *.par, *.txt, *.csv file Copy - copy table and results to clipboard Print - output table and results to printer Recent list - read one of the recent files (up to 9) Exit - exit the program, also use F12
This menu includes the operations with lines; convenient keyboard commands are also available.
Undo - undo the last line or edit operation
Cut - cut current line or field selection
and copy data to clipboard
Copy - copy current line or field selection
to clipboard
Paste - paste a copy of line, field selection
or table data from clipboard
Insert - insert empty line in current place
Edit - input data or edit a field in the
current line
Select - select/unselect line for calculation
Set phase - set a phase number or class for a line
Select phase - select the lines of current phase,
unselect other lines
Select all - select all lines with complete data
Invert all - invert selection of all complete lines
Copy selected - copy selected lines to clipboard
Copy all - copy all table lines to clipboard
Clipboard - show or edit current content of clipboard
Sort - set the column and direction for sort
This menu allows to set the different specimen-related data and conditions of diffractometry.
Specimen - input the information about specimen
Emission - select the emission from the list
or input the wavelength manually
Lattice type - set the syngony (Bravais type)
for specimen or current phase
Cell centring - set the Bravais cell centring
Correction - set angles of standard substance
for 2θ correction; set precision
Font - select the font for main screen
Options - see or change the configuration
of the program
This menu allows to perform different calculations available in the program, like lattice parameters, theoretical angles or indexing.
Parameters - calculate lattice parameters
by selected lines of current phase
Details - show chart and report of calculation,
recommendations for improvement
Density and 1/μ - calculate theoretical density
and attenuation length
Displacement - calculate specimen displacement
by minimal deviation of results
Lines by h k l - calculate cell data (V, c/a...) and
lines with known h k l
Generate lines - generate reflections by given
parameters, syngony and cell
Texture coeffs. - calculate texture coefficients
by Harris method
Indexing - find the possible indices of lines
in the table by shuffle method
By known h k l - find the possible indices of lines by
parameters calculated from known h k l
Results - show the results of indexing,
found by two criteria
Change indices - exchange indices of current phase
or invert indices with negative k
Mark lines as - mark lines as belonging to a phase
This menu allows to get the help and information about the program.
Context - help on current program mode or status General - table of content of this help system Check for update - check if the new version is available Manual update - update by a file of program archive About - current program version and developers
OS version: Windows XP or later, mouse
(Windows 7 or later is highly recommended).
Display resolution: 800×600 or higher.
Printing: paper size A4, font Lucida Console.
Internet connection: optional, it is used for update
and access to online resources in References.
Two archives can be downloaded on the RTP home page. Main archive rtp32.cab contains the program components and version history. Archive with test examples contains the diffraction tables of various samples or PDF data; some examples may help to understand the indexing process. All archives use a Windows cabinet (CAB) format and can be opened and unpacked in Explorer or in other programs working with archives. Before downloading, browser may show a warning about download of unknown file; you need to allow it. Such warning is a common precaution, never ignore it. Links to online security check are also available on the home page.
rtp32.exe - executable file (required) rtp.chm - help file (required) rtpwl.ini - wavelength list (optional) rtpam.ini - atomic masses (optional)
The main components of the program, rtp32.exe and rtp.chm, can be placed in any directory, which is not write-protected. Using the location, which is protected by operating system, like %ProgramFiles%, is not recommended. One of good places is the document folder in %userprofile%, such as C:\Users\Username\Documents\ (drive letter and username depend on your OS configuration). Here you can create a directory with specific name, like RTP or XRA, and unpack the CAB archive.
The files with wavelength list rtpwl.ini and atomic masses rtpam.ini are optional; if exist, they should be placed in the same directory. These files are not updated automatically because they may have specific user-defined data. Changelog history.txt is shown after successful update to inform about new options and fixes; you can also open it manually.
The shortcut to executable rtp32.exe can be created manually and placed wherever you want, e.g. on the desktop. To specify a directory with data files, input it in the "Start in:" field of the shortcut. The configuration file rtp.ini also will be saved in specified location. You can create several shortcuts to different directories and configurations. Launching the program directly in Explorer is also possible but not recommended if the data files are stored elsewhere, or when the program's directory may be write-protected because of read-only drive or no write permission for user account, so rtp.ini will not be saved.
Creating several shortcuts allows to start different program sessions (instances), when each session has individual configuration and works independently. Sessions can exchange the data (single line or whole table) using the clipboard, see the section clipboard operations for details.
Note: it is not recommended to place the program components in a directory with extended Unicode symbols, e.g. with Cyrillic letters; use the path with Latin characters and digits. Otherwise some problems may occur with the help system (you may not be able to open the help file independently).
After installation, it is recommended to check and change the options, which define your diffractometry: "Radius of detector circle" and "d of standard substance". You can also change other options, if need. This advice is shown when the program is started first time in a new location without configuration file.
Remark: the program may work with contrast themes, which can help people with non-perfect vision. In Windows 10/11 it can be set in Settings > Accessibility > Contrast themes. To follow the theme, set the "system" scheme in the options. You can also improve the contrast of main menu and UI elements only in this program. Open the properties of rtp32.exe file, select on the Compatibility tab the option "Reduced color mode": 8-bit (256) color.
Program does not keep specific information in Registry; all configuration is stored in rtp.ini. To uninstall the program, simply delete its components including the files used for update, rtp32.cab and rtp32upd.cmd, and created shortcuts. If you want to move the program to another machine, make a copy of all components and diffraction data to external drive (it would be better to copy the files with directory structure), then transfer these files to new PC. Finally, create new shortcut(s) on the desktop.
Check for update is accessible in the "Help" menu. It checks the build date and time on the program's home page; if the more recent version is available, you can Update it directly from the program. Make sure that all lattice calculations are performed and results are saved, if need. If the update was successful, the text file with the list of changes history.txt will be shown in the Notepad editor. You can close it and open the updated program as usual. Updates may include new operations, improvements and corrections of found errors.
Check for updated version can also be performed automatically on regular basis, daily or weekly. This setting is available in options; the date of the last check is stored in configuration file (dates of update use the calendar of your PC, they are not related to build dates).
If PC has a problem with Internet connection, you will see an error message. Try to check the connection using a web browser, then try to open Home page in the "About" dialog. In some configurations, Windows Firewall may block the Internet access for any program not included in the permission list, so you can check and download new version only in a web browser. Another possible error may happen if the new files cannot be saved. Check if the directory with the program components is not write-protected and has the write permission for current user account.
If Internet is not available or a machine is not connected to network, you can perform manual update by a local copy of main program archive. This file, usually rtp32.cab, can be downloaded on any machine with Internet connection and transferred, for example, by a portable drive. To download the file on a mobile device, use the QR code to the program's home page in the "About" dialog.
Update can be started from the "Manual update" menu. You need to select the downloaded *.cab archive in the file window. Please note that archive of currently used version is stored in the program's directory, so choose the new archive instead. If you prefer to unpack the archive and update each file separately, note that at least the files rtp32.exe and rtp.chm should be replaced with new versions. Do not replace rtpwl.ini if you have changed it by including your own wavelength list; the same is true for the list of atomic masses rtpam.ini.
Remark: if you choose rtp32.cab archive located in the program's directory, the files rtp32.exe and rtp.chm will be replaced with current versions. You can repair the broken files this way, but it may be better to browse the archive and replace the files using Explorer.
Configuration file stores the program settings and list of recent files; it uses UTF-8 text format. It is created in a working directory and updated upon exit, if you worked with files or changed any setting.
Almost all configuration settings can be viewed and changed in the options dialog, with exception of the last used wavelength, 2θ precision, font and delta. It is recommended not to change the file rtp.ini directly; use the program dialogs instead. Open this file in a text editor like Notepad only if need to check whether the current configuration might be a cause of a problem.
clock - clock on the screen: none=0, show=1
(can be changed by left-click the clock)
scheme - colour scheme: classic=1, retro=2, dark=3,
light=4, system=5 (follows desktop theme)
mark - mark of current field in the table:
none=0, dotted=1, solid=2, colour=3
update - check for update interval: never=0, daily=1,
weekly=2, date of the last check (dd.mm.yyyy)
font - name of font for main window, font size, style
(please change the font only in Font dialog)
lines - number of table lines visible on the screen
wave - last used wavelength, length unit (A or nm)
precise - last used 2θ precision
pdfprec - default 2θ precision for PDF-2 cards
precmode - precision mode: constant=1, cosine=2
delta - multiplier of 2θ precision for indexing
radius - distance from specimen to detector slit, mm
standard - up to 5 interplanar distances of a standard, Å
[recent] - list of the recently opened or saved files
Thank you for using this program and good luck in the researches using the X-ray diffractometry! Any opinions about the program, information about possible problems, issues as well as other useful recommendations will be received with gratitude.
Basic ideas and some code used in the program were developed in late 1980's by staff of X-ray research laboratory of the Institute of Inorganic Materials in Moscow: Andrey V. Golubev, Michael A. Poddyakov, Konstantin I. Avertsev, Iaroslav N. Chebotarev.
K. Avertsev — ideas and algorithm of the shuffle method used for indexing.
A. Golubev — ideas and algorithm of generation of indices for different lattices and cells centrings.
M. Poddyakov — first version of the program, basic code of solving the matrix using the Gauss method, calculation of lattice parameters up to monoclinic.
Ia. Chebotarev — calculation of triclinic lattice, 2θ correction, user interface, help system, Win32 version of the program, calculation of theoretical density and specimen displacement.
Calculation of attenuation length 1/μ is based on the C code developed by P. Bandyopadhyay and C. U. Segre, which is available on the Mucal periodic table web page [8]. The more recent update of the data published by A. Shaltout and others [9] has been applied as well.
Contact in Telegram messenger: @Slavic (please ask questions about the program without icons or stickers which can be counted as spam).
Below the list of authors is placed the QR (quick-response) code which directs to the program's home page, where you can find the current release and download the program archive on a mobile device. Information about loaded ini files, if they present in the program's directory, is also shown here: number of wavelengths in rtpwl.ini and number of atomic masses of the chemical elements and specified isotopes in rtpam.ini.
RTP files · PDF-2 files · AMCSD files · Text files · Winfit · Adding data
Select a data file from list (change the directory or drive if necessary). By default, here are shown the RTP data files in formats *.par and *.htm created by this program, *.aid exported from the PDF-2 database [1] and *.dif saved after the search of American Mineralogist Crystal Structure Database [2]. You can also select the text files *.txt in any acceptable format.
Supported file formats are described below. The same formats are accepted if you import the table using copy and paste clipboard operations.
Files *.par contain all common data available in the program interface: the table of reflections, calculated parameters, specimen structure, description and notes; this is a default format. Hypertext *.htm files contain the same information with added HTML code, which allows to see the data in a web browser. In addition, they show the non-reliable data in colour similar to the table on the program screen. Both file types use UTF-8 text format.
These files include both 2θ and d for each line; 2θ are counted primary as experimental data. If d exists but 2θ is missed, the line is incomplete; most likely an angle cannot exist at wavelength stored in the file.
Import of the PDF cards *.aid (saving a card in this format is an option in PCPDFWIN software) depends on the information in a particular card. For the most of modern cards, the program inputs the table of reflections (d, I and h k l) and calculates 2θ using the wavelength stored in the card. The substance name and additional data, such as space group, chemical formula and number of formula units, are input as well and can be seen in the specimen dialog; the units and formula are also shown in the density and 1/μ dialog. However, some old cards (before 1970) may have lack of specific data: no indices, no wavelength, undefined structure or formula etc. In such case, you will see a warning. Some cards may have too low precision of d, then the program reconstructs the precision of 2θ instead of default value. Otherwise the precision is taken from the options, field "Default PDF precision".
These are the files with diffraction data of minerals in the format of American Mineralogist Crystal Structure Database [2]. After searching the online database, use the link "DIF File" to save the file with the name composed from mineral name and database record number, for example, Jadeite__0000147.dif (monoclinic NaAlSi2O6).
The program imports the reflection table, which includes both d and 2θ, but for these files d values are counted primary and 2θ are calculated after import, usually with 3 decimal signs (original 2θ have only 2 signs). The name of mineral and space group are copied to specimen information. Precision by 2θ is used the same as for PDF files: "Default PDF precision" in options. Lattice type in these files is not specified directly, only a space group, so the program makes conclusion from the list of lattice parameters.
These files usually do not contain the chemical formula of the mineral. Sometimes the formula may present in the title of referenced publication in the file header. When opening a file, program looks for the formula and copies it to the specimen information, starting from the field "1". Besides this case, formula can be found on the AMCSD page with the database search results, under the title "Ideal IMA Formula". Here you can copy it to clipboard and paste to the theoretical density dialog.
AMCSD files do not have the number of formula units, which is required to calculate theoretical density and attenuation length. Instead, they include the density of the mineral (in g/cm3), which can be used to get this number from the molar mass M and cell volume V (see details in the formula units section).
Remark: before migration to RRUFF.net domain in the second half of 2025, the page with search results was noticeably different. Downloadable files with diffraction data used the name AMS_DATA.txt; however, file format was not changed. Existing AMS files can be opened in RTP as before, by selection "Text files" in the Open dialog, or you can change their extenstion .txt to .dif.
By selecting the *.txt files in the drop-down list below the file window, you can import a file with the list of 2θ or d and some additional data. This list may include optional header with the specimen name and wavelength, beginning from ";" or "#". File format may be plain ASCII or Unicode, both UTF-8 and UTF-16 encodings are supported.
Any data line must have 2θ or d value. Intensities and indices h k l are optional. Such files can be created manually or by the programs processing the raw data from XRD devices; header can be added later.
; Nickel FCC ; 1.54051 A 44.51 100 1 1 1 51.85 40 2 0 0 76.37 20 2 2 0
You can copy this and next examples directly to the program: left-click inside the example area, then use the "Paste" operation in the "Line" menu or on the toolbar, or press Ctrl+V key. Choose the data type of the first column in the "Select the data type" dialog, like 2th value in this example.
The data files may have different extensions, depending on the program from which the diffraction data were exported. For example, the program Match! may export the list of d and I values (File, Export, Peak data) to a file with extensions .dif or .csv. You may rename such file to *.txt or select the option *.* in the drop-down list. Here is an example of exported data file of Zr powder (hexagonal lattice, emission Cu Kβ, original format without header):
2.806608 281.7 2.579302 315.4 2.465013 1000.0 1.897778 205.0
If the file has a header with wavelength, it will be used to calculate 2θ or d (see below). To avoid possible problems with uncommon wavelength, you can optionally add the length unit "A" or "nm" after the value (see the first example). If other information presents in the header, it will be counted as a specimen name and additional notes and stored in the specimen information, up to 4 lines of notes. If no header exists (as in the second example), the file name will be used as a specimen name. After the input, you can change the information lines manually.
The diffraction data, either imported from a text file or pasted from clipboard, usually are not ready immediately for lattice calculations. You should perform some steps before and after the import.
Check the wavelength
Before the import, it is recommended to check current emission and change, if need. Also pay attention to the length unit. You can skip this step if the wavelength is included to the file header, but if the length unit is not specified, the program uses the heuristic approach to determine it (see details in the select the emission section). Otherwise, if the wavelength is not included, like in the second example, select it manually. You can skip this, but if the emission is not the same, you will have to set it later and recalculate d or 2θ.
If the wavelength is not included to the file, import logic will try to determine the length unit and may show a warning to prevent possible problem. If current unit is different than in the data, you need to Cancel the import and switch the unit in the emission menu, then open the file again.
Select the data type
Import logic attempts to determine whether the first column may be 2θ or d by the values in first 3 data lines (do they increase or decrease, are they more or less than 10.0 etc). This logic is heuristic and sometimes may make incorrect conclusion, especially if the file has less than 3 lines or if the wavelength is different from current. Import dialog shows the conclusion and first lines. You should choose the correct type: 2th value or d value.
Add required data
To use the imported data, you need to select the lattice type and set precision by 2θ. Initially, precision for common text files is taken from the last value input in the dialog correction and precision, field "Set 2th precision". You can set the appropriate precision before or after the import. Incorrect value will result in wrong precision of lattice parameters and may prevent indexing. Default value is 0.01 degree (suitable for both examples above).
To calculate parameters, input the indices h k l if they do not present (like the second example). You can also try to obtain them using the indexing process.
Import logic can recognise the data from *.txt files, saved in a text editor like Notepad after pasting the data from the clipboard of the Winfit! program [3], where the list of peaks was obtained after fitting the raw XRD data (Winfit does not have the direct option of writing these results to a file). The name of the file with raw data is shown in the first line, the program uses it as a specimen name; the integral intensities (Area) are imported to the "I" column.
Alternatively, these data can be pasted directly from Winfit using clipboard.
Sometimes you may need to combine several data sources with reflections from particular areas of diffractogram into one integrated table. For example, some areas may be obtained at different time; some raw processing programs may have a limitation by the number of points per single fit etc. Another example, when you need to have two data sets in the table, is the calculation of texture coefficients.
This operation works either for the data saved in files or copied to clipboard.
Text files
Data from common text files (with 2θ or d and intensity) can be added to existing table without limitations. When you open a *.txt file, if the table is not empty, the dialog asks, whether to Clear current table and then load new data (this is a default action), or keep the table and Add new data after the end. Dialog also shows several first lines of this file. For added data, the specimen name and other information will not be replaced, only new file name added to recent list.
In particular, you can add this way the Winfit! data from *.txt file or clipboard, when you have obtained the list of peaks in one of several diffraction areas.
New file may have a wavelength in the header, and if it is different from current or has different length unit (Å or nm), a dialog will show the remark about that. Imported data will be recalculated to current wavelength. Without wavelength in the header, if the supposed length unit in a file is different from current, you will see the warning in the dialog. If this conclusion is correct and the units are different, you need to Cancel the import, switch the unit in the emission menu and open the file again.
Newly imported lines always get the ordinal numbers in the table. If you want to differentiate them from previous lines, you can mark current lines as a phase with certain number before adding.
After the import, it would be a good idea to check the specimen information and add some notes about the table, if need.
RTP, PDF-2 and AMCSD files
These files cannot be combined directly: besides the diffraction table, they contain other data such as specimen information, crystal structure, lattice parameters etc., which would be lost in such merging. Because of this, the table is always cleared before opening a new file of this type. The exception is a preparation to calculate the texture coefficients, when the table already has the lines of a standard substance, marked as (s): you can add the specimen lines from another file in *.htm or *.par format.
To add the lines from a file in any format, you need to use the second program session and clipboard. Start another session of the program, open the file and select the lines which you want to add (by default, all lines with complete data are selected). It is recommended to check that wavelenght and length unit in both sessions are the same. Then copy selected lines (or all table) to Windows clipboard. Switch back to main session and use the "Paste" operation, then "Add new data" in dialog. Lines in the clipboard will be pasted after the end of current table, then you may close the second session.
This menu allows to clear the entire table and calculated results ("Clear all" or "New table" on the toolbar, default option), when only the wavelength and structure remain, or clear the particular parts of data. If you suppose to use current data later, save the table to a file before this operation.
Other options allow to clear:
— table data
Clear the entire table and keep the lattice parameters (if you generate the reflections by current parameters, the existing lines will always be cleared);
— specimen data
Clear the specimen information: name, all notes including the database reference and chemical formula, molar mass, density and attenuation length. Remark with information about 2θ correction (if it was applied) will remain;
— non-selected
Clear the table of non-selected and empty lines. This can help to clear the table of the lines, which are non-reliable or belong to other additional substances;
— phase labels
Clear all phase labels and numerate the lines in ascending. The information about structure of different phases will be lost. The lattice type and cell centring of last calculated phase will be assigned to all lines. If no phase was calculated, the structure of the phase with lower number will be taken;
— basic marks
Clear all marks of the lines as basic for indexing, if you want to select other basic lines;
— indices h k l
Clear the indices, if you want to input different indices or use indexing by shuffle (first successful indexing cycle will update the indices). If the table has more than one phase, you can choose whether to clear All indices or only the indices of Current phase with marker;
— 2th, d, I
Clear these data, if you want to apply the existing indices to new substance. In particular, you may use a previously calculated specimen, PDF or AMCSD card as a structure prototype to calculate angles 2θ and d for known h k l (this calculation deletes the precisions but keeps the intensities). If the table has more than one phase, you can choose whether to clear All these data or only the data of Current phase with marker;
— results
Clear the calculated 2θ, deviation and lattice parameters, if you want to perform different calculations (in any case, new calculations will overwrite the previous results). Note: if you clear both the table data and results, only the specimen information will remain.
You do not need to clear all data to calculate another specimen or phase with the same structure. Instead, you may input new 2θ or d values in the existing lines, change the specimen name and delete extra lines if need, then select the lines for calculation.
You attempt to clear the table when current data have never been saved to a file. For example, if you have input the experimental data manually or generated the reflections by lattice parameters — all data will be lost. If you suppose to use current data later, save them to a file first.
This operation may be non-interactive or may show the "Save as" dialog. It is performed silently if you already have opened or saved a file *.htm or *.par. Otherwise you need to interact with the file dialog first.
To save the table and calculated results, input a file name and select the format *.htm or *.par in the drop-down list below file window; the extension, if not specified, will be added automatically. Change the directory or drive if necessary. You can also select any existing file and use its name as a pattern or overwrite it.
If the table has not been saved and filename does not yet exist, the specimen name will be set as a suggested filename in the "Save" dialog. You can use it as is or edit if need.
The files *.par have a conventional UTF-8 text format, format of *.htm files is HTML. They contain all information about specimen, wavelength, full table of reflections and results of calculation if it was performed. They do not include some specific details visible in the program interface; the same limitations are applied to the printed tables.
You can save (export) the table data in different formats: *.par, *.htm, *.txt and *.csv. Choose the appropriate format in the drop-down list below the file window.
Formats *.par and *.htm are preferred for saving the data; besides the table, they store the information about specimen, wavelength and the results of calculations. Text-like format *.par is being used since old program versions, while hypertext format *.htm is more modern and has been added later. Hypertext contains the same text data with added HTML code, which allows to view a table in a web browser. Like on the main screen, it shows in colour the indices, which should not present in current lattice, and significant 2θ deviations (more than 3 × precision).
ASCII *.txt format is useful for phase analysis. This format contains the header with specimen name and wavelength, followed by the data lines with 2θ and I values (if no any intensities are known, 100 will be set instead). Use an option "Import ASCII" in the phase analysis program to import this table.
; Nickel FCC ; 1.54051 44.510 100.0 51.850 40.0 76.370 20.0
CSV (comma-separated values) file format is compatible with spreadsheets, for example, MS Excel. The table is exported completely, and calculated data are placed after the end of the table. This option allows to perform additional calculations, comparisons and visual presentations. Usually the files with .csv extension can be opened in the installed spreadsheet by default.
This operation copies the table and calculated results to Windows clipboard in the text format, which is the same as format *.par. You can use it to paste the results directly to written report or article without saving a file. You can also paste current table and results in other program session. This operation can be called from the menu "Table" or by command Ctrl+B. To see the copied table, call the clipboard content dialog by Shift+V command.
Confirm the output of the table and calculated results to printer. You can select a printer and change the printing preferences using the standard Windows interface. When ready, press OK to start printing.
Printing is implemented on basic level: it can help in common work, but cannot create a presentation-quality report (you can save the table to a file *.par and import it into a convenient text or presentation editor). The table is printed in black-and-white mode: the colour marks of large deviations and non-permitted indices, if they present, are not reproduced. Printing uses the monospace font Lucida Console, font size 14 points, regular style. Page layout is designed for A4 paper in portrait orientation, margins 15-20 mm; US letter size is also suitable.
Another option to have more control on printing is to save the table and results in HTML format and open it in a web browser. Most browsers, like Google Chrome, have an option to show a preview of the pages before printing, change the layout, margins and scale (zoom level) and are able to print in colour if the table has such marks.
Check whether the table and calculated results have been written to a file, if necessary. This warning is shown only if you have some unsaved data.
# ‹h k l› 2th ±2th d ±d I 2th calc deviation 1 1 1 1 44.510 0.020 2.0338 0.0009 100.0 2 200 3
Table with diffraction data is the main part of the program interface. It has several columns for experimental data, which can be input and edited manually or filled by the data from a file, and two colums for the results. Any line in the table represents the diffraction line of the investigated specimen. When input manually, the fields (table cells) are usually filled in consequently line after line, but you can change any data in any order, if need.
# - line number or phase, coincidence, basic mark
(to change, use menu by "Ins" or left-click)
h k l - Miller indices of the line
2th - diffraction angle 2θ in degree
±2th - precision of 2θ in degree
d - interplanar distance in Å or nm
±d - precision of d (usually calculated from ±2th)
I - intensity in detector counts or relative value
2th calc - angle 2θ calculated from lattice parameters
deviation - difference of experimental 2θ from calculated 2θ
To calculate the lattice parameters, fill in the fields: h k l, 2th and ±2th or d and ±d. Intensities are optional, they do not affect the results. To input or edit the data in a field, move the horizontal marker to chosen line using a mouse wheel or arrow keys on the keyboard, then left-click the field or press Enter key. You can also use the arrow keys to select the field: the header of current column is marked with the pair of angle brackets. In addition, mark of current field can be selected in options.
The lines, which have enough data for calculation, become selected by default and are marked by bluish background , which means that these lines will be used to get the results. For indexing, the indices may be skipped (and such lines cannot be selected for lattice calculation), but the intensity values, if known, may be very helpful.
If the indices h k l are marked by yellow , they do not correlate with current lattice type or cell centring (see more details in these sections).
Adjacent lines with the same 2θ and d values (they may have different indices h k l or belong to different phases) are automatically marked with the group marks to the right from the line number or phase label; they look like a big square bracket. This makes easier to see the coincident lines, especially in the results of indexing.
Enter - input a value, go to the next field/line Esc - restore value in the field, exit editing Tab - go to next field Shift+Tab - go to previous field Shift+Right, Shift+Left - select characters in the edited field Del - delete selection (also Backspace) Ctrl+X - cut selection and copy it to clipboard Ctrl+C - copy selection to clipboard Ctrl+V - paste selection in current place Ctrl+Z - undo the last field edit operation
Left click - edit a field in current line;
- input field value if clicked outside
of edited field within current line;
- cancel if clicked on another line
or out of the table
Right click - show the context menu for editing;
- input the value if clicked outside
of edited field within current line,
cancel if clicked on another line;
show context menu for clicked line
If you press Enter key to input the values in the fields, the program logic will attempt to assist your input. For example, h k l values less than 10 may be input without spaces. If the number of digits in the next index is the same or less than in current, the digits can be input "naturally", like 122 (1 2 2), 1014 (10 1 4) etc. However, if the number of digits in the next index is more than in current, need to add 0 before current index, like 08122 (8 12 2). For zero index, one zero is enough (see more details in the table below). If you are not sure, whether the conversion will be correct, use spaces to separate the indices.
In the first line, after the input of 2th and ±2th, the d and ±d fields will be filled in automatically according to current wavelength, and the field "I" (intensity) will be skipped. (If you want to input intensity, use the Tab key or left-click that field.) In the next lines, only 2th value is required, the precision ±2th will be copied from the previous line or calculated depending on your precision mode (see correction and precision). You can change the suggested value and input a value of your choice instead.
Undo operation (Ctrl+Z or "Undo" toolbar button) can reverse the last change of a field or line. It works separately for editing of a field and for line operations. In a field, any change can be undone once to a previous value; second undo restores the last value. Operation with a line (Edit, Cut, Paste, Insert) can be undone in normal (non-edit) mode. In particular, after editing a line you can exit the edit mode and restore all previously changed values in this line; it may help if you occasionally deleted or modified a field. However, changing any field in another line will make undo of previous line non-possible. See the section clipboard operations for more details.
Input Converted Digits Notes hkl h k l 3 any every h k l has 1 digit hhkl hh k l 4 non-zero hh, k, l 0kkl 0 kk l 4 from 0 0 for h, kk, l 00ll 0 0 ll 4 from 00 0 for h, 0 for k, ll hhkkl hh kk l 5 non-zero hh, kk, l 0hkkl h kk l 5 from 0 0h for h, kk, l 00kll 0 k ll 5 from 00 0 for h, 0k for k, ll hh0ll hh 0 ll 5, 0 inside hh, 0 for k, ll 0h0ll h 0 ll 5, two 0 0h for h, 0 for k, ll hhkkll hh kk ll 6 any every h k l has 2 digits
Example: suppose that you need to input the indices -1 10 2. If input directly without spaces as -1102, it will be interpreted as -11 0 2 because two digits for h have a priority, then the last 02 will be assigned to k and l. To input two digits for k correctly, need to provide two digits for h first: -01102. Now -01 will be assigned to h, then 10 to k and the last 2 to l.
# h k l 2th ±2th d ±d I 2th calc deviation 1 1 1 1 44.510 0.020 2.0338 0.0009 100.0 2 2 0 0 51.850 0.020 1.7618 0.0006 40.0 3 2 2 0 76.370 0.020 1.24596 0.00028 20.0 4
Selected lines are marked by a colour: they have a bluish background or green background with the marker at least until the "I" column. You cannot select the lines with errors or incomplete data; they will have a white background until correction. Excluded lines also cannot be selected.
On the illustration, the lines 1 and 2 are selected, while the line 3 is not. Marker is placed on the line 1, its right part is yellow because the results are not yet obtained. Note that the line 3 has a bluish line number: it shows that this line is ready to be selected, unlike the empty line 4.
Lines can be selected or unselected in many ways: by the "Space" key, in the context menu shown by right-click (press and release the right mouse button), by left-click the line in the column "deviation". The last way may be useful after calculation of parameters, if the lines are sorted by deviation. Click the values marked by colour to unselect these lines and improve the results.
Space - select or unselect current line
Shift+Up,
Shift+Dn - select/unselect a sequence of lines
Shift+Home,
Shift+End - select/unselect the lines from current
line to top or to end of the table
Enter - input or edit data in the current line
Ins - select phase number or class for current line
Ctrl+X - cut current line and copy data to clipboard
Ctrl+C - copy current line to clipboard
Ctrl+V - paste data from clipboard to new line
Ctrl+I - insert an empty line in current place
Ctrl+Z - undo the last line operation
Ctrl+L - select all lines of current phase,
unselect other lines
Ctrl+A - select all lines with complete data
Ctrl+T - invert selection of all complete lines
Shift+C - copy selected lines to clipboard
Shift+A - copy all table lines to clipboard
See above the keys for editing data in a field.
Left click - set the marker at pointer position;
- show the phase menu in "#" column;
- edit a field in columns from "h k l" to "I"
if clicked within current line;
- select/unselect line in "deviation" column
Right click - set the marker at pointer position
and show the context menu for a line
Wheel - move marker within the table, then scroll;
scroll the table if marker is outside
Shift+wheel - scroll the table
Initially all lines in new table, which is created manually or by import of diffraction data, do not have any special labels besides a line number. This is a common case when the table includes only a single phase. But if the number of phases is more than one, you can use the labels to differentiate the lines. In particular, you can mark the lines of the standard substance or separate two or more phases. Note that every phase has an independent lattice type and cell centring (primitive cubic type is assigned by default).
# h k l 2th ±2th d ±d I 2th calc deviation 2 2 0 0 51.850 0.020 1.7618 0.0006 40.0
✓ Numbers
Phase 1
Phase 2
Phase 3
Phase 4
Standard
Excluded
Basic |
To select a phase number or class for particular line, you can left-click the line in the column "#" or press the "Ins" to show the phase menu. Choose a label for this line:
Numbers - a line with ordinal number Phase 1...4 - one of specified phases, (1)...(4) Standard - a line of the standard substance, (s) Excluded - a line excluded from calculations, x Basic - a basic line for indexing
Selected phase is shown instead of ordinal number; a basic line has a dot mark "•" right of a line number or phase label (the excluded lines cannot be marked as basic). Please note: using the phase menu is not necessary — all labels can be set or changed directly by the corresponding keys, like key "1" to assign the phase 1 etc. Some advices related to selection of the basic lines can be found in the indexing section.
Total number of the lines marked as a standard (s) should usually not exceed the number of reflections of standard substance, which are defined in the options, maximum of 5. All available standard lines and their theoretical angles at current wavelength are shown in the correction and precision dialog. Additional lines cannot improve the correction, but can be used to calculate the standard as a separate phase.
Remark: to calculate texture coefficients, all lines with standard intensities should be marked as standard (s), while the lines of specimen should not have this mark. 2θ correction by standard lines cannot be used in this calculation.
Excluded lines do not participate in any calculation. Using this label may be reasonable if you want to mark them later as another phase, otherwise it would be better to delete ("Cut" in the "Line" menu) such lines. All non-selected lines can also be deleted in the clear menu.
Point at one of the lines belonging to a known phase, which you would like to calculate or define its lattice type or cell centring. Empty and excluded lines cannot be used for calculations. Please move the marker accordingly.
# h k l 2th ▲ ±2th d ±d I 2th calc deviation 1 1 1 1 44.510 0.020 2.0338 0.0009 100.0 44.502 0.008 2 2 0 0 51.850 0.020 1.7618 0.0006 40.0 51.857 -0.007 3 2 2 0 76.370 0.020 1.24596 0.00028 20.0 76.393 -0.023 4
You can sort (arrange) the lines in the table by phase numbers #, experimental angles 2th, interplanar distances d, intensities I and absolute values of deviations. To do this, left-click the table header with bright background. Alternatively, use the keys Alt + column number. The direction of sorting is shown by the triangle △ or ▽ in the chosen header, like by ascending of 2θ on the illustration above. By the second left-click, the direction switches to opposite etc.
Selection of the column and direction is also available from the menu "Line" or by the drop-down menu on toolbar button "Sort lines", which is also available by the Shift+R command. Key R allows to perform sorting immediately in specified direction or cancel it. Toolbar button also shows the sorting status: it looks pressed when the lines are in specified order.
Sorting is not repeated automatically: it is shown only when changing of the data in selected column does not break the specified order. This prevents the undesired change of line positions if the lines are edited or selected / unselected when the recalculation is active. To sort the lines again, left-click the header of chosen column or press the R key.
Remark: left-click the h k l table header calls the change indices menu.
R - sort the lines in specified direction Shift+R - set the column and direction for sort Alt+1 - sort by phase number, then by 2th Alt+3 - sort by 2th Alt+5 - sort by d Alt+7 - sort by I Alt+9 - sort by absolute deviation
In particular, sorting by deviations is useful after calculation of lattice parameters: it allows to see the lines with most significant deviation and unselect them or correct the mistakes in their data.
Sorting by phase is possible only if some of them were defined. The lines with ordinal numbers are sorted first, then the phases (1), (2) etc., then standard substance (s) and excluded lines " x ". Within any phase, the lines will be sorted by ascending of 2θ.
Operations with clipboard allow to cut, copy and paste different data using the common exchange buffer — Windows clipboard. It can be used with data within the program RTP as well as to transfer data to/from other programs. When used internally, the following operations are available with a text field, a single line, a group of lines or the table:
| Cut | Copy | Paste | |
|---|---|---|---|
| Field | Delete selected text and copy it to clipboard. | Copy selected text to clipboard. | Insert the copied text at current cursor position. |
| Line | Delete current line and copy it to clipboard. | Copy current line to clipboard. | Insert the copied line at current marker position. |
| Table | Cut is not available (use selective Copy and Clear instead). | Copy selected lines, Copy all table lines to clipboard. | Insert the copied lines after the end of current table. |
To see if a particular operation is currently possible, look at the toolbar buttons: available buttons are shown in colours and more bright, while inactive are more dim (some buttons may be hidden on the small toolbar), or open the menu "Line", where available operations are shown as active.
Field operations with editable fields in the table or in the dialogs are the same as in other text editing programs.
Line operations Cut and Copy can be performed with a line within the table (empty lines can be cut, but clipboard remains unchanged). Paste can be used at any marker position.
Table operations "Copy selected" and "Copy all" are available in the menu "Line", in the context menu by right-click within the table, or by keyboard commands Shift+C and Shift+A. The lines copied this way can be pasted only after the last line of current table. You will see a request, whether to clear current table or add new data at the end. After that, lines can be sorted or calculated with other existing lines.
Clipboard data can also be used to paste all lattice parameters to the dialogs calculate lines with h k l and generate reflections by parameters (see the first reference for details and examples).
Clipboard operations make easier data transfer from other programs to RTP for calculations and transfer back to use the results. Paste operation supports the same formats as input files: *.htm and *.par used by RTP, *.aid with PDF-2 data, *.dif with AMCSD record, several text formats including Winfit! clipboard or saved *.txt file and traditional 2th and I or d and I text data. Some formats are recognised automatically, some others show the dialog with first lines and a request, what is the type of data to import.
Important: to input all specimen information, most of formats require an empty table. If the table is not empty, you will see an information that paste will clear current table. If current data are important, you can Cancel the paste operation and save the table, or start another program session and paste the clipboard data there.
In particular, some examples in this documentation can be copied to clipboard by left-click and then pasted into the program. If you use data from other sources, like Internet pages or electronic publications, try to select the data lines accurately, especially pay attention to the begin of first line. Otherwise, this line or even all data may not be recognised or input incorrectly. In such case, you can open the clipboard content dialog and edit the lines manually.
While the more traditional way of transfer the table and results is saving them to a file, using the clipboard can also help in some cases. RTP uses the clipboard format with tabulation separators, which is compatible with spreadsheets like MS Excel. Operations "Copy selected" and "Copy all" add the table header before line data to make recognition of columns of the pasted table easier. Format of the header is almost the same as in the program interface (the Tab symbols are shown here as spaces):
# h k l 2th ±2th d ±d I 2th_calc deviation
Use Paste operation in a spreadsheet to work with table data. However, if you need the more detailed information, including the specimen name and calculated results, use the export in CSV format.
This dialog can be called by the operation "Clipboard" in the menu "Line" or by key command Shift+V. It shows a copy of current Windows clipboard in text format and allows to perform simple edit operations, such as change or delete some text (more advanced operations, search and replace, are not implemented; use an external editor like Notepad). Editing the text here does not affect the Windows clipboard: you can edit the original clipboard data and paste it to the table as many times as need. You can also update the clipboard after editing.
In particular, you can delete the symbols or lines which might occasionally be added after copy from external source, like electronic publication or web page, and keep only the required data. Sometimes a few extra symbols, even not clearly visible in a source, may prevent correct recognition of data.
Note: to input the tabulation symbol (Unicode 0x0009), use the key command Ctrl+Tab. Tab key alone selects the next button or text field.
Clipboard content dialog includes the operations:
Paste allows to paste current text directly to the table. If this is a copy of table data in the internal format or a copy of file in one of supported formats, it will be pasted to the table directly or with a request about the data type. This operation does not change the clipboard, even if you edited the text.
Update replaces the clipboard content with current text without pasting it to the table. This may be useful if you need to paste edited text in other place, for example, to the dialog of calculation of cell data and lines.
Clear deletes current content of clipboard.
This dialog is shown automatically when attempt to paste the clipboard data to the table was unsuccessful because the format was not recognised: you can correct current text and paste it here. If format is still not accepted, you will see the data format error message.
You can use this dialog whenever you want to check or edit the clipboard content. For example, after copy a chemical formula from an external document to calculate the theoretical density, you may have a problem to paste it to the "Formula" field (by Ctrl+V) because of invisible internal breaks or formatting characters in the source. Open this dialog, check and manually delete extra line breaks and unsupported characters, then update the clipboard. After that, formula should be pasted to the field correctly. The same approach can be used to edit the lattice parameters before pasting them in the calculate lines with h k l dialog.
Some program dialogs show the graphical and text data: in particular, stripe and scatter charts in the details of calculation dialog and graph of displacement in the specimen displacement dialog. These graphs can be copied to clipboard and pasted to any document, which supports graphical format, or to an image editor.
Use the context menu by right-click in the dialog area outside of selectable texts and choose what to do: "Copy image" with graph or "Copy text" with description and results. You can also access this menu by the Context key or Shift+F10 command. To copy only a part of text, select it by mouse, then use "Copy" in the context menu of selection or Ctrl+C command.
Clipboard can also be used to copy the lines from one program session to another. Single line is pasted at current marker position similar to local copy. When pasting group of lines, you need to answer whether to clear the table or keep it; lines are pasted at the end of the table. Warning is always shown when current and pasted wavelengths are different. While such transfer is possible, it is recommended to avoid it by using the same wavelength in different sessions.
Ctrl+X - field: cut selected text and copy to clipboard;
line : cut current line and copy to clipboard
Ctrl+C - field: copy selected text to clipboard;
line : copy current line to clipboard
Ctrl+V - field: paste copied text from clipboard;
line : paste copied line from clipboard;
table: paste copied lines at the end of table
Shift+C - table: copy selected lines to clipboard
Shift+A - table: copy all table lines to clipboard
Shift+V - show current content of clipboard (text only)
Shift+F10,
Context - field: show context menu with text operations;
graph: show context menu to copy image or text
In addition to keyboard commands, operations "Cut", "Copy" and "Paste" have the toolbar buttons on the normal toolbar (they are not shown on the short version of toolbar). To show the clipboard content, you can also click the button "Paste" with pressed Shift or use the menu "Line".
In this dialog you can input a specimen name and short description of specimen or its phases, if they are specified. These fields are optional: filling them in or using only a unique filename is a matter of personal style. Any line may have up to 68 characters or be empty.
Field "Name" is reserved for specimen name, it is also shown on the main screen (within the field length). When you read a PDF card or AMCSD file, a substance name is taken from the card. If you input the data of new specimen manually, name will be shown in the program title and used as a default file name when you save the table first time.
After input a PDF or AMCSD file, field "Notes" shows the card number and space group. Chemical formula in PDF card is copied to the line "1" (AMCSD cards rarely include a formula). If you input a formula in the theoretical density dialog, it will be stored in a chosen line. All non-empty lines will be saved at the end of the file *.htm or *.par.
Below the editable fields, some additional lines may be shown as well. One is a line with information about applied goniometer and specimen corrections: constant correction and specimen displacement. These data present only after correction by standard substance or calculation of specimen displacement. If you have calculated the molar mass of the formula unit and the theoretical density, they will be shown in another line. These lines are non-editable and will be saved to a file or printed as shown; you can select some text with mouse and copy to clipboard, if need.
Emission: 1.540600
Choose the emission type or wavelength from the list of emissions, which are commonly used in the X-ray diffractometry, in the "Emission" menu or by left-click on current value. You can also input the wavelength manually. The last used value is stored in the configuration file. This menu also allows to select the length unit: ångströms (Å) or nanometres (nm). If the length unit was changed when the table has some data, you need to calculate the lattice parameters again.
The internal table of wavelengths (which are more traditional than physically true) can be replaced with data from the file rtpwl.ini, which should be placed in the program's directory. This file can include up to 20 data lines, each includes the name, wavelength and short description. The example below is based on the work of G. Hölzer and others [4].
; Wavelenght list for RTP32 ; replaces the internal table (max. 20 lines) ; G. Holzer et al., Phys. Rev. A, 56 (6), 4561 (1997) ; Name Lambda Description &Cu-Ka1 1.540593 Emission of copper, line K-alpha1 Cu-K&b 1.392235 Emission of copper, line K-beta A&g-Ka1 0.559363 Emission of silver, line K-alpha1 C&o-Ka1 1.788996 Emission of cobalt, line K-alpha1 Co-Kb 1.620826 Emission of cobalt, line K-beta C&r-Ka1 2.289726 Emission of chromium, line K-alpha1 Cr-Kb 2.084881 Emission of chromium, line K-beta &Fe-Ka1 1.936041 Emission of iron, line K-alpha1 Fe-Kb 1.756604 Emission of iron, line K-beta &Mo-Ka1 0.709300 Emission of molybdenum, line K-alpha1 Mo-Kb 0.632253 Emission of molybdenum, line K-beta &Ni-Ka1 1.657930 Emission of nickel, line K-alpha1 Ni-Kb 1.500152 Emission of nickel, line K-beta &W-La1 1.476345 Emission of tungsten, line L-alpha1
You may create your own rtpwl.ini using this one as an example. All wavelengths should be input in ångströms (they will be shown in nanometres if you choose this option in the menu). If you use the non-Latin characters, like Greek letters, save the file in the UTF-8 format.
The program uses the heuristic approach to determine whether the manually input value is in Å or nm. Every value is checked against the values in the table within relative difference 0.00067 (the relative differences in the wavelengths listed in scientific media and databases usually are less than 0.0002). If the value is found, the emission type and its unit are determined as well. However, wavelength with relative difference more than 0.0002 is counted as non-standard (this is shown in the tooltip, see below).
If the wavelength unit is not specified and a closest value in the internal table is not found, the values less than 0.49 are counted as nm (for reference, less common Ag Kβ is about 0.49701 Å). If you use a rare short-wave emission like W Kα1 (0.20901 Å) or Au Kα1 (0.18020 Å), add it to rtpwl.ini to prevent a mistake in length unit.
Cu Kα1, Å |
Tooltip for the wavelength field at mouse pointer shows the name of current emission and the energy in kiloelectronvolts (keV); the energies for the emissions listed in the menu are also shown in the context tip on the screen bottom. This value may be helpful to estimate the thickness of diffraction area by chemical composition of the specimen (more details are in the calculate attenuation length section).
Energy of X-ray photon is calculated by the formula:
E = hc/λ
where h — Planck constant, c — speed of light, λ — wavelength. Coefficient hc is 1.23984198 eV·μm, this is equal to keV·nm.
There may be two remarks after emission name: (exactly) and (non-standard). First means that current wavelength is exactly the same as in the table; second shows that the relative difference from wavelength in the table is more than 0.0002. Both remarks are informational, they do not affect the calculations.
Input the specific wavelength for current experimental data, if it does not present in the common list. The last used value will be stored in the configuration file. Please read the details and recommendation in the previous section.
Lattice: A orthorhombic
Select the Bravais lattice type (syngony) for investigated crystal substance or phase in the "Lattice type" menu or by left-click on the syngony name. If the table has more than one phase, the current phase is defined by current position of the marker. When you add new phase to the table or assign new phase label to existing line, it gets the default "P cubic" type. Check this and correct for every new table or new phase, if needs.
For the rhombohedral, monoclinic and triclinic syngonies, where the negative indices are possible, the program checks if a particular negative h, k or l may be valid; if not, these indices will be marked in the table by yellow h k l . Check and correct the yellow indices accordingly.
For indexing, if a syngony is unknown, it is recommended to begin the process from the most symmetric types.
Select the Bravais cell centring for current lattice type in the "Cell centring" menu or by left-click on the centring letter. If some indices in the table should not present in the chosen centring because of extinction, they will be marked by yellow. The option "find highest" allows to find the most symmetric centring for all indices of current phase.
The program allows to select only those centrings, which are possible from the crystallographic point for current lattice type [5]. All other centrings are inactive and cannot be selected. In the practice of X-ray analysis, however, the less restrictive approach may exist, like, for example, a face-centred triclinic cell. They are not minimal or do not have the full set of symmetry translations, but sometimes these models may be useful to describe a distortion or phase transformation of more symmetric cells; they also may exist in some PDF cards. When the program opens such card, non-standard centring will be marked by yellow centring letter. This lattice still can be calculated, but if you change the centring, it cannot be restored back in the program interface.
In this dialog, you can input and calculate the data required for 2θ correction, change 2θ precision for all lines in the table, change the precision mode. To correct the angles 2θ, which may be shifted from ideal positions because of detector or specimen misalignment, you can use the experimental angles of standard substance. You can also correct the angles by calculated attenuation length in the material.
The required theoretical angles of standard substance are calculated from interplanar distances, which are stored in the configuration file, at current wavelength. Use options to see or change these data. Note that 3 decimal signs for calculated angles is only a visual limitation here, the program internally uses all available signs.
Standard #:
To use the standard substance correction, input from 1 to 5 experimental angles 2θ (see the technical details below). Single angle gives the constant correction; two or more allow to calculate the specimen displacement and correct the experimental angles of specimen more precisely.
Please note that usage of two or more standard angles is highly recommended; the constant correction by single angle may give reliable results only in narrow area around this angle.
Adding the lines of standard substance to the table is not required, but can be helpful. In this case, you can input their line numbers with "#" symbol, e.g. #4. You may input "#" without a number, then the line nearest to the theoretical angle will be taken. You can use this if the phase label (s) is assigned to standard lines instead of ordinal numbers (caution: the label is not checked here; if the nearest angle belongs to investigated phase, it will be taken instead of standard, so check the angle after calculation, when it will be shown in this field).
Press Calculate if you want to see the correction (constant and displacement values) without changing the table. Press Apply to correct the angles of all lines in the table. Calculated constant correction and specimen displacement / detector radius will be shown in the specimen dialog and saved as a remark in *.par or *.htm file.
Remark: if standard substance is applied on the surface of specimen, be sure that thickness of the layer is much less than attenuation length 1/μ in the standard (for example, 1/μ in diamond for Cu Kα emission is 0.67 mm). Otherwise, you may need first to calculate the cell volume of the standard and correct its 2θ angles by attenuation length.
2th rms deviation:
This root mean square deviation is calculated for 3 or more angles of the standard substance. After calculation of constant correction and specimen displacement, the angles of standard are compared with their ideal calculated positions. This value is not used anywhere directly, but can help to estimate the consistency of standard. It should be quite small, typically about 0.01 degree or less, close to goniometer precision. Higher deviation may be a result of incorrect separation of the standard and adjacent specimen lines or an input error. If so, consider to re-check these angles, but if the calculated correction and displacement are high too, need to check the goniometer adjustment.
Constant correction:
This field shows the constant (zero-point) correction of detector angle calculated by the lines of standard substance. You can also input here the constant correction for your detector manually and calculate the shifted angles.
In the contemporary XRD devices, the zero-point correction is applied automatically after goniometer adjustment or, if need, it can be input manually in the control software, so the experimental angles are already fixed and additional correction before calculation of parameters is not required. However, for old-style optical goniometers such correction still should be added manually.
Specimen displacement, mm:
This field shows the specimen displacement calculated by two or more lines of standard substance, in millimetres. A positive value means the shift of specimen plane toward the diffraction angle, negative — backward.
If you input the constant correction and/or specimen displacement manually, then Calculate will give the expected angles of standard substance for such misalignment. This may be useful to reproduce the alignment of specimen and/or adjustment of goniometer.
Specimen displacement can also be calculated independently by the minimal divergence of results of investigated material, in this case the lines of standard substance (two or more) are used only for constant correction. See calculate specimen displacement section for details.
Attenuation length, mm:
This field allows to input the attenuation length 1/μ in the investigated material at current wavelength. By default, it is empty and should not be input if the calculation of attenuation length has not been performed. After calculation of length, field shows it in millimetres. This correction is applied only once, then the field becomes empty until the next calculation of attenuation length.
Effect of the shift of diffraction angle from attenuation is quite small for 1/μ about 0.01 mm (10 mcm) and can be ignored for materials with lesser attenuation length or for layers with thickness much less than 1/μ. It should be taken into account in the materials with 1/μ about 0.01 mm or more, when the specimen thickness is significant.
Important: unlike the correction by the standard substance, which is applied to all lines in the table, this correction is phase-specific and depends on distribution of phases. For example, for uniform mixture of powders the correction calculated for the mixture is the same for all its components. However, for a thin layer this correction may be not applicable at all.
You can change the calculated value here, but generally, it is not recommended. However, it should be done in two specific cases. First, if you have calculated 1/μ in multi-component specimen externally (see an example how to calculate attenuation length for multi-phased specimen). Second, if you have calculated the theoretical angles from lattice parameters, you can invert the attenuation effect by adding the minus sign to this value to make the angles 2θ close to real diffractometry.
Set 2th precision:
Here you can change the precision for all lines in the table; this affects the results estimation and indexing. For a pattern, use "#" and line number, e.g. #2. Without a number, the first line will be taken as a pattern. Please note that in the cosine mode the precision of any line will depend on 2θ. If you set only the precision, the buttons Apply and Calculate are equal. This value is stored in the configuration file as "precise" and can be set without data in the table. Default value is 0.01 degree.
Precision mode: constant
This mode, constant or cosine, defines the suggested precision of 2θ when filling in the table as well as the precision which is set for all lines in this dialog. It also affects the calculation of root mean square deviation.
In the constant mode, the program suggests the same ±2th for all lines. This may be useful when the precision is mainly determined by detector step, whilst the diffraction lines are relatively narrow and 2θ range is limited.
In the cosine mode, the suggested precision depends on 1/cosθ. This is suitable for wide 2θ range and broadening diffraction lines. It decreases the relative weight and contribution to the results of the lines at large angles 2θ, which often are weak and less reliable.
Cosine mode should be used only for manual input of data in the table. When the data are input from a file, precision mode is returned to constant.
While this dialog allows to calculate both the correction data (constant and displacement) by experimental 2θ of standard substance or the expected 2θ of the standard by direct correction data, the priority of calculation depends on existing data and active field. If only experimental 2θ or only direct correction exist, the button Calculate performs the calculation of missed data — either the correction or expected angles of the standard, while the button Apply calculates the correction or takes existing direct values and applies them to lines in the table.
However, if some experimental angles and direct correction present at the same time, the priority depends on active field (the field with text cursor or selection). If the correction or displacement field is active, the dialog calculates all expected angles of the standard; if any other field is active, new correction data are calculated from existing angles.
Formula used:
correction = constant − 2·cosθ·displacement/radius
Constant (zero-point) correction should be added to all experimental angles to compensate the shift of detector from ideal position. Specimen displacement gives the correction depending on cosθ. Both these parameters are obtained using the least squares method from cosine — deviation data set. Calculation of displacement also uses the detector radius (typical value is 200 mm, see options).
Remark: this formula is slightly simplified, it does not take into account that the displacement changes the goniometer geometry and effective radius. However, the difference from strict calculation is far beyond of typical 2θ precision (about 0.0001 degree per 1 mm of displacement or even less).
This dialog shows the parameters, which will be used for correction of the angles 2θ after the initial data were input and calculated in the correction and precision dialog. Depending on these data, it may show the constant (zero-point) shift, specimen displacement and attenuation length 1/μ. While usually the constant correction and specimen displacement are applied separately of attenuation length, all three parameters may be used at the same time. Please note that the first two parameters affect all angles in the table, but the last is applied only to the angles of current phase, if the table has more than one phase, so set the marker accordingly. You can also Cancel this operation and input the correction-related data again.
This dialog allows to choose the font for main program screen. Font list shows the scalable fonts installed in your system. Initially the program uses the monospace font Lucida Console, font size 14 points (12 points on displays with low resolution), regular style. The chosen font name, size and style are stored in the configuration file.
The number of available fonts depends on version of your operating system, language and additionally installed fonts. However, not every font may have the symbols needed for program interface and description of phases. It is recommended to choose the font which has at least the Western and Greek symbols and your national alphabet, if need. Alphabets supported by each font are shown in the drop-down list "Script". Select the font carefully: while the most of commonly used fonts should look well, some decorative or handwriting fonts may be not clearly readable or the symbols in some fields may be improperly cut. You may select any available style, the size should be an integer value from 9 to 28 points.
Button Apply allows to change current font and see it on the screen without closing the dialog. After choosing the font, press OK to change it permanently. You can Cancel any change and restore previous font.
Selected font affects the size of the main program screen. If you want to change only the font size, it can be done without font dialog: use the keyboard or mouse commands shown below. You can also resize the screen by dragging the borders by mouse: the program will set the closest possible font and number of table lines for new screen size. Horizontal size may change from the width of small toolbar to the width of desktop, the number of lines — from 4 to 41. Dragging the sizing grip in the bottom right corner can change both the font size and lines on the screen.
Note: the font selected here does not affect printing, which always uses the regular font Lucida Console, 14 points.
Ctrl+(Num+) - increase font: zoom in Ctrl+(Num-) - decrease font: zoom out Ctrl+(Num*) - restore default font size Ctrl+wheel - zoom in / zoom out
Here you can see and change the settings which are stored in the configuration file rtp.ini. Default choices are shown for reference.
Colour scheme: system
You can choose a scheme for main program screen: classic, retro, dark, light, system. Classic is the original scheme, shown on the illustrations in this help. System scheme automatically switches between dark and light, following current desktop theme; it is recommended for high contrast themes (can be set in Windows accessibility settings).
Mark of current field: none
This option allows to change the look of current field in the table, which can be directly edited by Enter or F2 key. The choice none does not mark this field, dotted or solid show the border around it, colour shows the field with the distinct coloured background. Find a combination of scheme and mark, which is better suited your visual perception.
Auto update check: never
Program can check for update automatically on regular basis: never, daily, weekly. This check performs one time when the program is started without opening a file. If new version is available, you will see the information about this and can decide whether to update now or later. Set automatic check only if your PC has a stable Internet connection, otherwise use manual check in the "Help" menu. Note that new program versions are being released not very often, so weekly check may be more reasonable.
Default PDF precision: 0.010
The cards exported from PDF-2 database may not contain any specific information about precision, so this value is used as default 2θ precision; it is also used for AMCSD data. More exactly, PDF cards may have different presumed precision, depending on the number of significant digits in the d values. Modern PDF cards, including the theoretically calculated, have at least 5 significant digits, so this default precision, typical for modern XRD equipment, is applied to these data. However, some old cards may have only 3 or 4 significant digits (the rest of digits required by format are zeroes). The program checks this and can restore the approximate 2θ precision basing on significant digits of d and wavelength; in such case the default precision is not used. When importing AMCSD data, this default value is used to calculate precision by d.
Radius of detector circle, mm: 200
This is a distance between specimen and first slit of detector, in millimetres. It allows to calculate the exact value of specimen displacement by two or more experimental angles of standard substance in the correction and precision dialog. It is also used for calculation of 2θ correction by attenuation length. It does not affect other results.
Standard #:
You may input from 1 to 5 interplanar distances of external standard, used for calculation of 2θ correction. Diffraction angles of the standard are calculated at current wavelength and shown in the correction and precision dialog. All distances here should be input in the current length unit (Å or nm), which is set in the emission menu.
Default built-in data: natural diamond at 25°C [6]. Replace this if you use a different standard like alpha quartz, magnesium oxide etc. To restore the default values, clear or input 0 in all 5 fields.
; Natural diamond at 25C, a=3.566986 A ; T. Hom et al., J. Appl. Cryst. (1975) 8, 457-458 ; d h k l 2.0594003 1 1 1 1.2611200 2 2 0 1.0754867 3 1 1 0.8183227 3 3 1
Calculated results · Precision and divergence · Deviation · Quality
To calculate the lattice, the lines must have non-empty h k l and 2th. Use the "Calculate" toolbar button or F6 key to calculate lattice parameters by selected lines of current phase. If the table has more than one phase, the current phase is defined by current position of the marker. To calculate other phase, move the marker to any line of that phase first.
Before the first calculation, please make sure that you have set the correct emission and lattice type of current phase.
Name: Nickel FCC Emission: 1.540510 Lattice: F cubic Parameter precision divergence Parameter precision divergence a= 3.5232 0.0010 0.0005 V= 43.734 0.036 0.018 2/3 2th rms dev= 0.007: very well # h k l 2th ±2th d ±d I 2th calc deviation 1 1 1 1 44.510 0.020 2.0338 0.0009 100.0 44.502 0.008 2 2 0 0 51.850 0.020 1.7618 0.0006 40.0 51.857 -0.007 3 2 2 0 76.370 0.020 1.24596 0.00028 20.0 76.393 -0.023 4
After successful calculation, the lattice parameters, their precision and divergence are shown in the top window; the calculated 2th angles and deviations are added to the lines in the table. The common results of lattice calculation are the parameters and cell volume. For some lattices the relation c/a is also calculated, and for orthorhombic lattice — the split rate (b-a)/(b+a).
Errors (uncertainties) of any calculated parameter are described by precision and divergence. Precision is an error caused by the limited precision of the original data: ±2th or ±d, while divergence is a result of difference between the ideal calculated lattice and real experimental data. Because of different nature, precision and divergence can be counted statistically independent.
Precision, in most cases, is limited by instrumental errors and quality of determination of peak position, which is limited by profile width. It can be improved by more precise measurement of diffraction angles, which includes the instrumental errors of diffractometry (goniometer precision, instrumental broadening due to horizontal and vertical divergence of X-rays and collimation, specimen shape and thickness), improving the statistical reliability (reasonable angle step and exposition time, signal/noise and peak/background ratio), increasing the number of lines used for calculation and careful separation of overlapped lines.
Divergence can be improved by excluding the outliers (see details of calculations) and more precise alignment of specimen, but for better improvement, if possible, need to understand the physical factors of the difference from ideal lattice model.
In the lines used in calculation, the columns 2th calc and deviation show the calculated theoretical position of 2θ for the indices h k l and the difference of experimental 2θ from calculated 2θ. For non-selected lines of the same phase, which do not contribute to calculation of lattice parameters, the values 2th calc and deviation are shown inactive (pale).
If the experimental data and lattice type are correct, for the most of lines the deviation should not significantly exceed the precision.
The deviation values more than 3 × precision are marked in the table by yellow. If a single line or small part of all lines show the significant deviation, it may be a result of accidental error or mistake. Consider to unselect such lines from calculation: left-click the line in "deviation" column (in other words, click the deviation value) or press the "Space" key. However, if the total number of lines with high deviation is significant, it may be a result of the systematically poor data (experimental precision is not as good as ±2th in the table), bad specimen alignment, incorrect separation of overlapped lines or the lines of another phase, or incorrect lattice type.
12/14 2th rms dev= 0.015: very well
The line below the parameters shows the quality of the results. Quality is estimated by comparison of the root mean square deviation of 2θ (2th rms dev) with the root mean square experimental precision (see the estimation section in the quick reference).
Two numbers separated by slash to the left from the estimation show the number of lines used in calculation and total number of lines of current phase. Their background shows the recalculation mode: bluish if this mode is active (on the illustration above) and common background if the recalculation is not active. Recalculation is also shown as the pressed "Calculate" button on the toolbar and in the main menu. When the recalculation is active, the results will be immediately updated after any selection or unselection of the lines of current phase. Recalculation becomes inactive after any operation, which changes the data in the table. To cancel the automatic recalculation, press "Esc", or press "Calculate" again, or left-click these numbers with mouse.
It is recommended to keep the automatic recalculation active, then you will be sure that the lattice parameters correspond to current data in the table.
Space - select/unselect line for calculation
Shift+Up,
Shift+Dn - select/unselect a sequence of lines
Ins - set or change a phase of current line
Left click - set the marker at pointer position;
- show the phase menu in "#" column;
- select/unselect line in "deviation" column
Right click - set the marker at pointer line
and show the context menu
The main algorithm is based on the method of least squares. The system of linear equations is obtained from original data using the classic Bragg law. The resulting matrix with dimension equal to parameters number of current lattice is solving using the Gauss method. The errors, which are due to 2θ precision, are obtained from the solution of this matrix. The errors due to the divergence between the calculated model and original data are obtained by solving another matrix, which is composed by deviations between calculated and original 2θ.
The angles 2θ are calculated from lattice parameters using the standard equation for interplanar distances (1/d2) for current lattice type.
Stripe chart · Scatter chart · Statistics and recommendations
This dialog can be called by the "Details" toolbar button or in the main menu after successful calculation of lattice parameters (otherwise, it suggests to perform the calculation first). It has the chart, some statistical information and recommendations.
Chart shows the distribution of deviations among all lines used for calculation. It allows to quickly see the lines with significant deviation (outliers). Areas of the chart have the different colours corresponding to the intervals of root mean square experimental precision by 2θ with multipliers:
green - area within 1 × precision green yellow - areas within 2 × precision yellow - areas within 3 × precision orange - areas beyond 3 × precision
Chart has two modes: stripe and scatter. Stripe chart is shown by default; to switch to the scatter chart, select the check box "Show the scatter of deviations".
Statistics and graphical data are not available for the results with zero or very small divergence, as for theoretically calculated 2θ. It would look like a single line on the chart, which cannot help to estimate the quality of diffractometry.

On this chart, labels on axis X show the deviation in degree among the calculated lines. Labels on axis Y are not displayed, if the intensities of the lines are not known. If they present, axis Y shows the intensities in logarithmic scale, by default from 1 to 100, or more, if there are lines with higher intensities (for example, from 1 to 999 in the PDF cards with theoretically calculated data). Labels at the top border show the multipliers of experimental precision of the coloured areas, it may help people with non-perfect colour vision.
Vertical dashed line shows the mean deviation (it counts the +/- signs, unlike the root mean square deviation). This line should be near zero on the axis X, usually within goniometer precision. Significant shift means that the distribution of deviations is asymmetric (skewed).
If the shift is more than either 0.5 × precision or 0.05 degree, you will see additional warning message below of statistical data. This may be a result of specimen displacement (most often) or the zero-point shift of detector. It is recommended to adjust the specimen in goniometer and repeat the diffractometry, or at least calculate the displcement and correct the angles 2θ.
If the shift of distribution is less than above but more than 0.1 × precision or 0.01 degree, you will see additional information (as on the illustration). While such shift may not require re-adjustment of the specimen, it is recommended to calculate and apply the specimen displacement to improve the results.
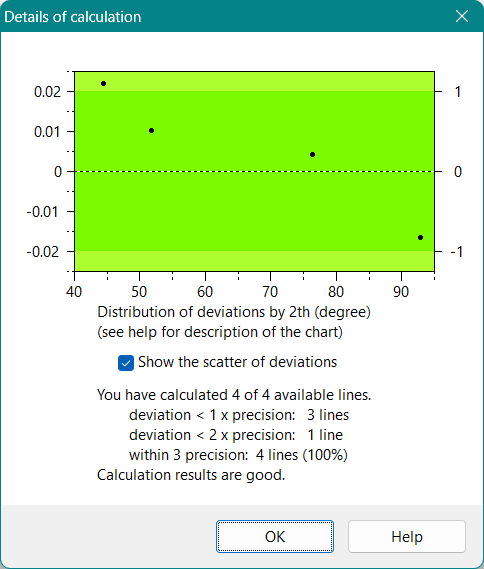
In this mode, axis X shows the angles 2θ, while axis Y shows the deviation, both are in degree. Like on the stripe chart, the areas are marked by the colours, but because of different axes X and Y, colour areas are horizontal. Mean deviation is not shown here, line at zero level is a divider for convenience. Scatter pattern of the dots allows to estimate the results in different way than on the stripe chart.
In particular, specimen in correct position gives near horizontal distribution of the dots, while a misalignment results in a slope: rising trend is caused by a negative specimen displacement or negative shift of detector from zero point, while falling trend (like on the illustration above) means that the displacement or zero-point shift is positive. Curved distribution, usually with local minimum, may be an indication that current phase has a significant attenuation length.
Remark: if the scatter of deviations is mostly a result of statistical errors rather than specimen position or XRD state, the pattern may be less informative than the mean deviation on the stripe chart or the graph of specimen displacement.
Statistical information below the chart shows the number of lines with different absolute deviations as shown on the chart — less than 1 × precision, less than 2 × precision, less than 3 × precision and the total number of "good" and "bad" lines.
Dialog informs whether the results are good. If not, you can attempt to improve them by unselecting some lines with too high deviation (lines with deviation more than 3 × precision are marked in the table by yellow in the "deviation" column).
Important: before unselecting the lines, be sure that the position of specimen in goniometer was correct, otherwise attempts to improve calculation may give wrong parameters. Check the specimen displacement and look at the result: significant displacement means that it may be reasonable to check the goniometer adjustment and realign the specimen.
To find all outliers, close this dialog and sort the lines by deviation. Alternatively, follow the program's suggestion by pressing Unselect button.
Remark: you do not need to unselect all suggested lines. Always look at the estimation of results; sometimes unselecting only a few outliers may significantly improve the results. At least you should unselect the lines until no lines left in the "orange" areas.
If the number of outliers is big and the results are not good and cannot be improved this way, you should verify the experimental data: indices h k l, angles 2θ and lattice type. You can also revise the experimental precision ±2th and assign more appropriate value to the lines.
Dialog also shows the information if the table has some not yet selected or unselected lines of current phase with the deviation within 2 × precision, and suggests to Select these lines, which may statistically improve the results. Use such suggestion with caution: the program does not know anything about the physical state of the investigated substance, it estimates the result basing only on formal principles. For example, you might intentionally unselect some lines, which supposedly belong to another phase (like a distorted or transformed lattice). If you mark these lines as a different phase, the program will no longer suggest to select them.
Chart can be copied to Windows clipboard. Right-click the graph and select "Copy image" or "Copy text" in the menu. Image will be copied to clipboard, then you can paste it to a document, which supports graphical format, or to an image editor. Copied image remains in the clipboard until the next copy operation.
You can also copy the text description of the chart and statistical data. Use the menu or select some text by mouse, then use "Copy" in the context (right-click) menu of selection or press Ctrl+C.
Formula units · Chemical formula · Format · Calculation
This operation allows to calculate the theoretical (X-ray) density of the material by the chemical formula and calculated cell volume. Dialog of calculation of the density is also used to calculate the attenuation length of an element or compound.
Theoretical density is a density of the material with ideal defectless crystal structure; it is often used to evaluate the changes in the crystal structure after the phase transformation or doping by different elements and is also used as a value which the density of real material in monocrystalline form with minimal possible amount of defects and impurities should approach to.
Remark: for this approach, structure non-uniformities such as replaced or irregular atoms in the substitutional or interstitial solid solutions are not counted defects, as long as they are included to the formula unit, unlike the intercrystalline and intergraine voids, atoms which do not present in the formula or additional phases.
Calculation of theoretical density uses the chemical formula of the compound, which gives the atomic composition, the number of formula units in the crystal cell, which is a structure unit, and atomic mass of the elements, which gives the molar mass:
ρ = z·M/(V·NA)
where ρ is the density, z is the number of formula units in the cell, M is the atomic mass of the formula unit (molar mass), V is the cell volume,
NA is the Avogadro number, 6.02214076·1023 1/mol.
Remark: traditional symbol of the number of formula units is capital Z, which is the same as the symbol of atomic number. To avoid ambiguity, this documentation uses the small z letter for the formula units.
Theoretical density can be used to estimate the fraction of internal voids and impurities in the solid materials or the porosity in the materials pressed from powder, for example, in powder metallurgy. For empty pores filled with air or gas, the porosity φ is:
φ = 1 − ρexp/ρ
where ρexp is the experimental density and ρ is the theoretical density.
When porosity is more than about 0.1, it is recommended to count it in calculation of attenuation length for better 2θ correction. See below how to calculate attenuation length for powder phase.
Atomic masses of the elements used in the program are mostly taken from the PubChem open chemistry database [7]. File rtpam.ini, if exists in the program's directory, replaces the internal table of atomic masses partially or entirely. It has two lists: common list with all elements in the current (2026) periodic table and list of isotopes. Common list in the file included in RTP archive is the same as internal, and if these data are suitable for your work, you may not add it. If you prefer some more traditional or more precise masses, add rtpam.ini and replace that data in a text editor or include only those elements to your file.
List of isotopes presents only in rtpam.ini. It has the masses of some commonly used isotopes and serves mostly as an example; it may be extended and include up to 30 different isotopes. Here are the data lines from both lists for comparison:
;Number Mass Symbol ;common elements 26 55.845 Fe ;isotopes 26.55 54.9382934 55Fe
Number in the common list is the atomic number Z, while in the isotope list it also includes the mass number A separated by dot. Mass is the atomic mass in g/mol, statistical mean of the masses of naturally existing isotopes or the mass of the most stable isotope in the common list and exactly known mass in the isotope list. Symbol in the common list is the chemical symbol of element, while in the isotope list it is the combination of mass number and chemical symbol. Symbols in this file are used for reference; the list of chemical symbols is built in the program.
To use an isotope in a formula, need to enclose its symbol in round brackets, like (55Fe). Brackets are important, otherwise the number will be counted as a multiplier instead of mass number. If an isotope does not present in the list, the mass number will be used as atomic mass (with loss of precision).
Remark: using the square brackets for an isotope is not recommended, because this type of marking is used for selectively labelled compounds (not supported in the program), where the isotopes, written directly before the formula, are not the part of composition.
To calculate the density, algorithm needs the number of formula units per one cell, which should be input in the theoretical density dialog, field "Units". It can be known from the description of particular structure or taken from the structure prototype. Here are some examples:
simple cubic 1 (8·1/8) BCC, HCP 2 (8·1/8+1) FCC 4 (8·1/8+6·1/2) C (diamond) 8 (8·1/8+6·1/2+4) CsCl 1 SiO2 (α-quartz) 3 NaCl, CaF2 4
Initially this field is empty. Number of units is not required to calculate the molar mass M from the chemical formula, but required to calculate both theoretical density and attenuation length. Most of PDF-2 files have this number, it will be set automatically after opening such file. AMCSD files do not contain formula units, but include the density of the mineral.
If you open AMCSD file, the program reads the stored density and shows it on the screen bottom when you open the theoretical density dialog:
AMCSD: rho = 3.774 g/cm^3
If you keep the field "Units" empty and input only the formula, the program will use the density, molar mass M (from the formula) and cell volume V (from lattice parameters) to calculate the number of units. If the formula has been found in the AMCSD file, it will be shown in the "Formula" field. Then you can Calculate the units and get the result immediately.
You can also input the number manually, it will be used as initial data.
After calculation of density, number of units can be stored in the line of specimen information after the formula, separated by two slashes as a comment. If the calculation of density is performed again, the formula will be shown in this dialog as well as the stored number.
Remark: sometimes the information about the number of units or atomic positions in the cell may be not easy to find. If so, this number may be determined empirically. Assume that the cell has one unit: input number 1 and calculate what the density would be in such case. Then take the experimental density or measure it using a laboratory equipment and divide by the calculated value. The nearest integer (usually slightly greater than the result) is the number of units.
Formula of chemical composition (formula unit, molecular formula) or the list of atoms and their amount in the unit is required to calculate the molar mass. Program is able to decrypt the typical formulae and count the atomic composition. Sometimes, but not always, the formula may be found in the information about specimen, or it can be input manually. To input the formula, select any empty line and type the formula or copy it from the source and edit if need.
PDF cards usually include the formula, it is copied to the description line "1". Drop-down list "Formula" shows the lines of specimen information starting from "Notes" and allows to select such line.
AMCSD files include the formula, if it is mentioned in the title of publication. In such case, the program reads the formula and shows it in this dialog. Formula is always specified in a separate data file or is shown in the database search results (see AMCSD files section for details).
Formula should be input in one line without subscript or superscript characters; additional spaces may present for clarity. It may have up to 16 chemical elements; specific isotopes are counted as separate elements. Be careful about letter case and similarly looking symbols. Always check the atomic composition after decryption of the formula to avoid mistakes.
If a formula have the brackets, they are limited to 4 levels of nesting and should be paired; only the round ( ) and square [ ] brackets are supported; the braces { } are not. State of aggregation should be removed: all substances are expected to be solid (s) or crystal (cr). Valence, oxidation state and charge numbers are not supported and should be removed from the formula too.
For example, SO42− ion should be written as SO4.
The centre dot sign, which separates the components such as hydrates, double salts or double oxides, may be any of these (Unicode # is for reference):
* asterisk 0x002A · middle dot 0x00B7 • bullet 0x2022 ∙ bullet operator 0x2219 · dot operator 0x22C5
When you input a formula manually, use the asterisk key * on keyboard; other variants are mostly used in electronic publications. Do not use the common dot (period) which is reserved as decimal dot. Centre dot is required when need to separate the multipliers of the components, for example, in blue vitriol CuSO4·5H2O
Numbers of elements or groups in the brackets may be non-integer, like for non-stoichiometric compounds, mixtures or substitutional solid solutions. For numbers less than 1, zero must present before the decimal dot. Formulae with the variable composition like olivine (Mg,Fe)2SiO4 cannot be properly decrypted; the proportions of the components should be clearly specified.
Examples of formulae:
Al2(SO4)3 aluminium sulfate (55Fe)3O4 iron-55(II,III) oxide Ca2[B5O9]Cl*H2O hilgardite[2]
Remark: some non-standard signs or elements of structure formula are accepted but not recommended: they are added to decrypt formulae from external sources. Multiplication sign × may be used instead of centre dot. Minus signs - or en dash – or equal sign = may show the molecular bonds: all of them are counted as spaces between different parts of formula. Plus sign + may be used only on basic level as a separator of components in chemical expression, is cannot be used inside the brackets.
After input of all required information in the dialog, press Calculate button. You will see the line with atomic composition and the line with result: molar mass M in g/mol and density ρ in g/cm3. Attenuation length 1/μ, calculated for current wavelength, is shown in millimetres. If the formula cannot be properly decrypted because of error or complexity, you will see an error message and need to correct it until the error disappears.
If the cell volume V or number of formula units is not known, only the molar mass can be calculated. Lattice parameters and volume are calculated automatically in this operation, if the table has only a single phase. You can input the number of units manually or, in the case of AMCSD file, input the chemical formula to calculate the units.
Remark: you can calculate the density without diffractometry data. Select the lattice type and input the lattice parameters in the calculate cell data and lines with h k l dialog, which gives the cell volume even if the table is empty.
After successful calculation, press Store to keep the formula and number of units in the selected line of specimen information. By default, this is the line "1" in the specimen dialog. Result of calculation will be added to the information list in a separate line.
Example: calculation of the density of zircon (tetragonal structure, attenuation length is calculated for Cu Kα emission)
a = 0.6607 nm, c = 0.5982 nm, z = 4
Units: 4
Formula: ZrSiO4
Atoms: Zr 1; Si 1; O 4
Result: M = 183.305 g/mol, rho = 4.6626 g/cm^3,
1/mu = 0.0262 mm
Remark: to reproduce this calculation, clear all data, set the emission and lattice type, then copy the line with parameters to clipboard. Open the dialog calculate cell data and lines (Alt+A): parameters will be pasted here and you can calculate V and c/a. Open the dialog of calculation of density (Alt+M), input the formula and press Calculate button.
You can copy the data and calculated result to clipboard. Right-click in the dialog area outside of selectable texts and use "Copy text" in the menu.
Single element · Crystalline phase · Powder phase · Multi-phased
This operation uses the same dialog, which calculates the theoretical density.
Attenuation length 1/μ is the thickness of a material where the intensity of X-ray emission on the surface decreases in e times (to about 37%), where e is a base of natural logarithm (2.71828...) and μ is the linear attenuation coefficient. Knowing this length is important to estimate the thickness of the area analysed by X-ray diffractometry. In particular, it can be used for more precise 2θ correction.
Two types of calculation of the attenuation length 1/μ are implemented in the program:
Decreasing of the intensity of rays in the depth of a material from initial intensity on the surface at normal incidence is described by the Beer-Lambert law:
I = I0·exp(−μx)
where I is attenuated intensity, I0 is initial intensity, x is the length.
Linear attenuation coefficient μ depends on the photon energy E (it is shown in the tooltip to wavelength) and atomic number Z. The dependence is non-linear and includes the atomic photoeffect, coherent (Rayleigh) and incoherent (Compton) scattering.
For multi-component specimen, μ is additive and can be calculated by the formula:
μ/ρ = ∑ wi·(μ/ρ)i
where μ/ρ is the mass attenuation coefficient of mixture or compound,
wi is the mass proportion of the component i in the specimen,
(μ/ρ)i is the mass attenuation coefficient of the component i.
Remark: calculation of attenuation length implemented in this program is based on the code and data available on the Mucal periodic table web page [8]. Original data, where some elements are missing, have been updated with more recent data [9]. Currently the elements 1...94 and X-ray emissions with energies from 5 to 100 keV are supported (including all wavelengths in the list of emissions).
Besides the parameter 1/μ, which is defined for normal X-ray incidence, the parameter of attenuation of diffracted ray depending on angle θ can also be useful — the depth of the half of diffracted intensity, where the integral intensities of the diffracted rays from the layers above and below are equal:
d1/2 = sinθ·ln(2)/2·1/μ ≈ 0.35·sinθ·1/μ
This formula is used to calculate 2θ correction for current phase by its attenuation length in the correction and precision dialog.
Effect of the shift of diffraction angle from attenuation is somehow similar to the specimen displacement, but the shift depends on θ with the maximum around 45 degree due to multiplier sinθ·cosθ — at the small angles the diffraction depth is low, at the large angles the angle shift of depth is low. The shift is quite small for 1/μ about 0.01 mm (like titanium at Cu Kα emission, see below) and can be ignored for materials with lesser attenuation length or for layers with thickness much less than 1/μ.
For example, for Cu Kα emission (E = 8.048 keV), the 1/μ in aluminium (Z = 13) is about 70 μm, in uranium (Z = 92) — 1.7 μm, so the half diffraction depth for θ = 30° is about 12 μm and 0.3 μm, respectively. For the more short-wave Mo Kα emission (E = 17.480 keV), the half diffraction depths are about 130 μm and 1 μm.
This calculation is performed when you input a symbol of single element in the "Formula" field and when the calculation of lattice parameters was not performed (parameters are empty). "Units" field is not used in this calculation. Chosen element is assumed at standard temperature and pressure in the most stable phase state. Note that some elements at standard conditions are gases or liquids.
Calculation shows the molar mass M of chosen element in g/mol and attenuation length 1/μ in mm, the same as in the correction and precision dialog.
Example: calculation of the attenuation length in titanium at Cu Kα emission (titanium has the HCP structure with 2 atoms per cell, this value is not used here).
Units: Formula: Ti Atoms: Ti (in normal state at standard conditions) Result: M = 47.867 g/mol, 1/mu = 0.0110 mm
Remark: if the main table has some diffraction lines and the lattice parameters were calculated, you may clear only the parameters but keep the table by using the "Clear", "results" menu or toolbar button. This also clears the calculated 1/μ in the "Correction and precision" dialog.
This calculation is performed with the calculation of theoretical density. You need to calculate the cell volume, input the number of formula units in the cell and chemical formula. All elements in this calculation are counted in the crystal state; the atomic density of particular element is calculated by division of the mass of atoms in the cell by the cell volume. The structure of phase is supposed to be close to ideal: no impurities, very small intercrystal defects and voids.
Powder state means the presence of voids between crystalline particles, which are filled with transparent gas or air; they increase the attenuation length. Volume part of voids can be defined by porosity φ. Effect of voids can be calculated as equally decreased amount of all elements in the formula with coefficient 1−φ in the same cell volume. To input the common coefficient, use brackets around the formula.
Example: calculation of the attenuation length for Cu Kα emission in the specimen of magnesium oxide MgO with porosity 0.15 (MgO has a cubic structure of NaCl type): a = 4.212 Å, z = 4
Units: 4
Formula: (MgO)0.85
Atoms: Mg 0.85; O 0.85
Result: M = 34.258 g/mol, rho = 3.0452 g/cm^3,
1/mu = 0.113 mm
Important: molar mass M calculated this way is a parameter of imaginable structure where all atoms are partially substituted by vacancies. It may be unstable or non-existing, so do not use this value in other calculations. However, both parameters ρ and 1/μ describe the real powder state.
Calculation of attenuation length for a specimen composed from several phases is not implemented directly. You need to use an external software like a spreadsheet to get the result from data calculated in the program.
Calculation uses the formula for multi-component specimen, where each component presents a separate phase, and may include porosity for powder state. To prepare initial data, calculate the parameters ρ and 1/μ separately for each phase. See an example below for explanation.
* * *
Example: calculation of the attenuation length for Cu Kα1 emission in a specimen pressed from powders of aluminium oxide Al2O3 and zirconium oxide ZrO2 in mass proportion 60:40 with porosity 0.2.
First, need to get the density and attenuation length for components. In this example, the known lattice parameters of minerals are used, but in practice, they should be calculated from diffraction data of real materials.
Al2O3 (corundum) has the hexagonal structure, cell contains 6 layers (units) along the c axis: a = 4.7591 Å, c = 12.9894 Å, z = 6
Units: 6
Formula: Al2O3
Atoms: Al 2; O 3
Result: M = 101.960 g/mol, rho = 3.9871 g/cm^3,
1/mu = 0.0795 mm
Low-temperature ZrO2 (e.g. baddeleyite) has the monoclinic structure with 4 units per cell:
a = 5.1505 Å, b = 5.2116 Å, c = 5.3173 Å, beta = 99.230, z = 4
Units: 4
Formula: ZrO2
Atoms: Zr 1; O 2
Result: M = 123.222 g/mol, rho = 5.8096 g/cm^3,
1/mu = 0.0166 mm
Now you can copy the calculated ρ, 1/μ and also w, 1−φ (if presents) to a spreadsheet and add required formulae. First two values can be copied to clipboard directly from the "Result" line by selecting a value with mouse and then "Copy" in the right-click menu or by Ctrl+C command.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | Phase | rho | 1/mu | w | w/rho | w*mu/rho |
| 2 | Al2O3 | 3.9871 | 0.0795 | 0.6 | 0.150485 | 1.892897 |
| 3 | ZrO2 | 5.8096 | 0.0166 | 0.4 | 0.068852 | 4.147684 |
| 4 | ||||||
| 5 | rho_mix: | 4.559197 | ||||
| 6 | sum_w: | 6.040581 | ||||
| 7 | 1/mu_mix: | 0.036311 | ||||
| 8 | 1-phi: | 0.8 | ||||
| 9 | 1/mu_spec: | 0.045388 |
In this table, cells with formula are marked by blue (replace with A1 reference style, like = w / rho with =D2/B2, = SUM(w*mu/rho...) with =SUM(F2:F3) etc.):
w/rho = w / rho (for each phase) w*mu/rho = w/rho / 1/mu (for each phase) rho_mix = 1 / SUM(w/rho...) (sum of all phases) sum_w = SUM(w*mu/rho...) (sum of all phases) 1/mu_mix = 1 / (sum_w * rho_mix) 1/mu_spec = 1/mu_mix / 1-phi
Remark: to see this example in a spreadsheet, click here to copy the text with formulae to clipboard. Then paste it to cell A1 in the spreadsheet.
For each phase (component of the mixture), need to calculate w/ρ, which allows to get the density of mixture, and w*μ/ρ, a part of the sum. Using the density and the sum of parts, you can get the 1/μ of the mixture in crystalline state without pores. If the specimen has significant porosity, as in our example, the result should be divided by 1−φ.
To correct the lattice parameters, copy the calculated 1/μ from the spreadsheet to the "Attenuation length" field in the correction and precision dialog and apply it to 2θ angles of current phase. If the table includes other phases of this mixture, apply 1/μ for each phase and recalculate the lattices.
Calculate displacement · Results and correction
In practical X-ray diffractometry, the diffraction planes of investigated material are usually differ from the goniometer plane by the value called specimen displacement. In a typical case of specimen alignment to a holder using a glass plate, the displacement may be only a few micrometres (μm), but if the specimen surface is not well polished and has some roughness or for powder specimens, the real displacement may be much more. Methods of internal and, more often, external standard substance placed on the specimen surface (like a diamond powder) are used to compensate such misalignment; this correction is supported by the program. However, such correction may be not ideal if the reflecting areas of specimen phase and standard substance are different.
Another way to find the displacement and compensate it uses the displacement model, which is applied to set of diffraction lines to find the position when the divergence of calculated results from ideal structure is minimal. If used properly, it allows to find the displacement with precision up to 1 μm. However, this operation should be used with care because improper calculation may result in additional uncorrectable errors instead. In general, it should be used only when the shift of the diffraction angles is a result of specimen misalignment and is not due to another reason like internal stress, phase non-uniformity, phase transformation etc.
Important: before performing this calculation, be sure that the constant correction (zero-point shift of detector) is close to zero, i.e. is no more than goniometer precision. Otherwise, the displacement will be calculated incorrectly, which results in wrong lattice parameters. If need, check the adjustment of goniometer or perform the diffractometry of a standard sample. If the constant correction is not zero but is known for current goniometer adjustment, input it manually in the correction and precision dialog. You can also calculate and apply this correction by two or more lines of standard substance (the displacement calculated by standard lines will be used only as a first approximation). Warning: correction by only a single standard line is highly undesirable and may result in additional errors.
Please note that calculations use the radius of detector circle as a base length. Check this parameter in options and correct if need.
Remark: 2θ correction by displacement calculated this way should be enough, if the attenuation length 1/μ is no more than a few micrometres. Otherwise it is recommended first to calculate attenuation length at current wavelength by chemical formula and porosity (for powder specimen) and apply it. Correction by 1/μ shifts the different h k l planes from the depth of half diffraction to specimen surface, which this correction shifts to the goniometer plane.
First, you need to calculate lattice parameters: it gives an initial value of 2θ root mean square deviation (2th rms dev) which is used as a starting point for next comparisons.
Initial dialog allows to set the limit by displacement in millimetres: this is an interval of calculation from negative to positive values (positive means the shift of specimen plane toward the diffraction angle, negative — backward). This limit can be from 0.005 to 2.0 mm, default value is 0.2 mm. Greater interval allows to find bigger displacement, but it increases the calculation time and the graph looks more rough; lesser interval makes the graph more fine. Anyway, if the found displacement is within the interval, the results will be the same.
Low limit, from 0.005 to about 0.05 mm allows to show the graph with high resolution, which is about 1 μm. Such small displacement is achieved by careful preparation of surface, good specimen alignment in goniometer and for materials with small attenuation length. Contrary, if the displacement is much bigger than the default limit, it may be because of rough specimen surface or wrong alignment; in the last case, the calculation of lattice parameters can only be used as a first approximation.
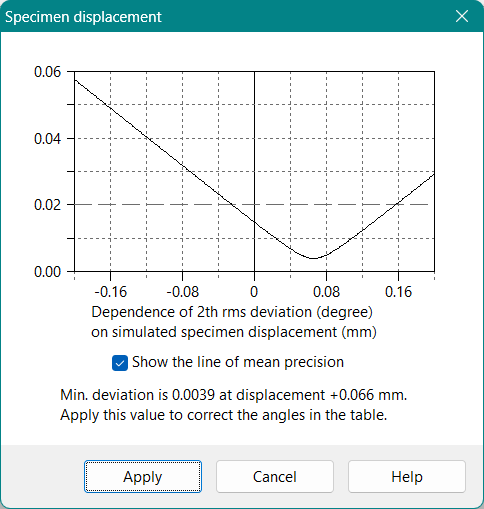
Dialog with the results shows the graph of dependence of the root mean square deviation by 2θ on the simulated specimen displacement. Axis X shows the displacement in mm, where current position is at zero point, axis Y shows 2th rms deviation in degree. Line of dependence should have a local minimum, if the displacement is within the interval, which is set in the initial dialog.
Check box "Show the line of mean precision" allows to show the horizontal dashed line at the mean experimental precision by 2θ. Position of the line can help to estimate the effect of correction: more significant, if current deviation is above this line, and less in other case. When the line is shown, the scale of Y axis may change, so unselect the check box if you want to decrease the limit of displacement or look at the dependence more closely.
Below the graph, you will see the information about minimal found deviation and corresponding displacement. If the difference between current and minimal deviation is very small and beyond of typical precision, this difference is also shown in round brackets.
Press Apply to correct the specimen misalignment, if it is significant (more than a few micrometres, depending on material). This will recalculate the angles of all lines in the table, not only the lines of currently calculated phase. Lattice parameters of current phase will be updated automatically; other phases, if they present, should be recalculated manually. The applied displacement will be shown on the bottom in the information about specimen dialog (along with constant correction, if it was used).
Please note that applied displacement cannot be undone immediately. If it was performed by mistake, reopen the initial table if it has been saved to a file before this operation. Alternatively, you can reverse the correction: look at the current displacement in the dialog information about specimen and input the inverse value in the correction and precision dialog, "Specimen displacement" field.
Sometimes you may see additional messages at the bottom of this dialog:
Specimen is in right position, no correction required
You will see this information if the found displacement is less than 0.001 mm or 0.2·1/μ. This is normal for all theoretically calculated lines or if the correction has already been applied.
Improvement of deviation is much less than precision
This message is shown if the effect of correction would not be significant, because the experimental precision is the main factor of uncertainty. It happens when current deviation is already less than precision and correction will decrease it by less than 10% of precision. Correction still can be applied to improve the calculation of lattice parameters.
Minimal deviation is at current limit of displacement
This happens if the found displacement is equal to current limit: minimum is reached at the border, which you can also see on the graph. Press Change and increase the limit in the first dialog. If the found displacement is large, about 1 mm or more, it is recommended to check the specimen alignment and repeat the diffractometry.
Minimum of deviation is somewhere outside of possible limit
This message means that supposed displacement is too large, more than the limit of 2 mm. You can apply current value and calculate displacement again, approaching the minimum step-by-step, but checking the specimen alignment is highly recommended. If it will have no effect, check the goniometer adjustment using the test samples and fix the problem, then repeat the diffractometry.
If need, this graph can be copied to Windows clipboard the same way as charts. Right-click the graph and select "Copy image" or "Copy text" in the menu. You can paste the copied image to a document or an image editor. Use this menu to copy the texts with description and results. You can also select some text by mouse and use "Copy" in the context menu or Ctrl+C command.
This operation allows to input the lattice parameters and calculate the cell volume V and additional (derived) parameters like c/a relation or orthorhombic splitting. Then it calculates 2θ and d values for the lines with indices h k l, if they present in the table. In particular, cell volume is required to calculate theoretical density and attenuation length.
The indices in the column h k l may be input manually, or be used from a previously calculated specimen, or from PDF/AMCSD card used as a structure prototype. Intensities of the lines, if they present in the table, will remain after calculation, which allows to use the existing data with new parameters. If the table has more than one phase, move the marker to any line of the chosen phase before input the parameters.
To perform calculation, first check the lattice type, then open the dialog by Alt+A keys or "Lines by h k l" toolbar button. Lattice parameters may be input manually or pasted from the clipboard (see the details below). Limits for edges a, b, c — 2...99 Å or 0.2...9.9 nm; for angles alpha, beta and gamma — 1...179 degrees (this is a formal limitation, in practice the angles usually are within the limits about 45...135 degree).
The fields in this dialog, as well as parameters fields in the generate reflections by parameters dialog, allow to input one of the arithmetic operators + - * / with two arguments. This may be useful to calculate the edges for a cell with multiplicities, based on multiple cells with simple structure, and vice versa. The original values may be a result of previous lattice calculation, which you need to multiply or divide. Examples:
2*5.348 or 30.609/3
Parameters can be pasted to this dialog from clipboard. Data in the original text, which is copied to clipboard, may be organised in different ways.
First, the parameters may be listed in traditional order without names, as a sequence of values divided by spaces. Such list can include either only independent parameters of current lattice (from 1 for cubic to 6 for triclinic), or all 6 parameters (3 edges and 3 angles). PDF and AMCSD cards always include 6 parameters for any lattice. Length units of edges may be ångströms or nanometres; you need to set this unit in the emission menu before copying. See two first examples below.
Second, the parameters may have the names and length unit for edges, for example, a=4.444A alpha=88.88. Angles may have either the Latin names or Greek letters, like β=123.4. Length unit should be specified for each edge, it may be ångström (Å or A, default unit), nanometre (nm) or picometre (pm), like a = 356.6986 pm. All values will be converted to current unit before being shown in this dialog. Such format is often used in the electronic publications and Wikipedia, see third example.
Text may also include the number of formula units in the cell, like z=6. This is optional and may help to calculate ρ and 1/μ: number of units will be copied to that dialog and you only need to input the chemical formula.
Important: before pasting, check that all current lattice parameters (calculated results or previously input in this dialog) are cleared, i.e. equal to zero, otherwise they will have priority over clipboard data. To clear current parameters, use clear results operation in main menu or key F8, "results". Operation "Clear all" (New table) also clears these data.
To perform calculation this way, set the lattice type, also check current length unit in the emission menu if the original data do not have the names and units of parameters. Copy the data to Windows clipboard and open this dialog: values will be pasted to corresponding fields. Information that parameters are pasted is shown in the status line at the screen bottom:
Parameters are pasted from clipboard
If this message is not shown, check again the clipboard and clear current parameters. You can check the clipboard data in clipboard content dialog by Shift+V or Shift+"Paste" toolbar button.
The examples below show the lists of lattice parameters in different formats (edges are in Å, remarks can be used to calculate ρ and 1/μ).
List of all 6 parameters for hexagonal lattice:
4.913 4.913 5.405 90.00 90.00 120.00 PDF-2 46-1045: hexagonal α-quartz SiO2 z=3
List of 4 parameters for monoclinic lattice:
9.4180 8.5620 5.2190 107.580 AMCSD 0000147: monoclinic jadeite NaAlSi2O6 z=4
List of named parameters with length unit for monoclinic lattice:
a = 5.1505 Å, b = 5.2116 Å, c = 5.3173 Å, β = 99.23°; Z = 4 Baddeleyite - Wikipedia: monoclinic ZrO2
If the list of parameters is much different from these examples, try to edit the clipboard data in the clipboard content dialog. In the complex case, you are always able to copy and paste all parameters separately, one-by-one.
Remark: parameters from this and next dialogs are not recalculated automatically after changing the length unit in the emission menu. You need to calculate them from lines or input the parameters in new unit again.
To calculate the reflections with generated indices h k l, first select the lattice type and set the cell centring, if it is known, or leave the type "P" (primitive). Then open the dialog (Alt+G), fill in the parameters and set the 2th range — minimum and maximum values of 2θ angles, 0.0 80.0 by default. Because the number of possible h k l combinations is limited by the table size (440 lines), the program will show warning if this limit exceeds and will decrease the upper 2θ value. If you want to get more results, look at the last calculated angle and use it as a starting point for new 2th range.
Limits for edges a, b, c — 2...99 Å or 0.2...9.9 nm, for angles alpha, beta and gamma — 1...179 degrees, for 2th range — 0...179 degrees.
About the arithmetic operations in the fields and using the clipboard see the previous section.
Requirements · Standard · Specimen · Calculation
Texture — anisotropic distribution of orientation of crystallines in polycrystal materials — is an important characteristic of machinery and engineering components, which affects their mechanical and thermo-physical properties. While the method of direct X-ray study of the texture requires specialised XRD devices, alternative and often time- and cost-efficient method is to get and compare the texture coefficients (TC) using the traditional XRD devices. Then they can be used to build the inverse pole figure (IPF). One of the ways to calculate such coefficients is the Harris method [10], initially developed for the bars made from α-uranium with orthorhombic lattice.
According to Harris, the texture coefficients can be calculated from the set of experimental and standard intensities by the formula:
TC(hkl) = Iexp(hkl)/Istd(hkl) / [1/N·∑(Iexp(i)/Istd(i))]
where TC(hkl) is the texture coefficient of orientation h k l, Iexp is the experimental intensity, Istd is the standard intensity (calculated or measured on powder specimen), N is the number of experimental reflections.
Some preparations should be done to perform this calculation. You need to have two data sets in the table:
Both lists should have 2θ or d: it allows to calculate the lattice parameters and avoid some mistakes. Selection of the lines does not affect this calculation.
While any data may be used as a standard, the best approach is to use a database of powder diffraction like PDF or AMCSD. To get the data, perform a database search and save the card as PDF-2 file in *.aid format or AMCSD file in *.dif format. Then open this file in the program and mark all lines as standard (use the "Mark lines" toolbar button or F11, "s" keys). Check the lattice type and presence of h k l and intensities. You can also calculate lattice parameters and verify the quality of this card (though the parameters are not used later).
Lines with experimental intensities can be added manually, but it would be better to have them in a separate file: you can add the data to existing table whenever need. You can prepare an RTP file in *.htm or *.par formats, or use the experimental data in the text format with 2θ or d, intensities and indices.
Text files with d values are somehow better than with 2θ: you will not need to recalculate the angles of specimen or standard if the wavelengths are different. While the angles are not used in this calculation, an option to calculate and compare the lattice parameters may be helpful.
When all lines of the standard are marked in the table as (s), the program counts the next opened file as the specimen data by default. You will see additional dialog only if the wavalengths of specimen and standard are different. In such case, you can calculate New 2th for specimen lines or Change wave and recalculate the lines of standard to specimen wavelength. This choice does not affect the results of texture calculation.
Important: to prevent mistakes, PDF and AMCSD cards cannot be added to the table as the lines of specimen. If you open such file, current table will be cleared and filled with the lines of new card. If you, by any reason, want to calculate a card as a specimen, open it and save in one of RTP formats.
When all required data are ready, use Alt+U command or "Texture coeffs." in the "Calculate" menu. Calculated coefficients will be shown in the "texture" column (in place of "2th calc" values). This column remains on the screen until any lattice calculation, so be ready to save or print the results. Usually the specimen lines with texture coefficients appear in the table after the standard lines. You can move them to the top by clicking the column header "#", which sorts the lines by the phase number.
If some problems happened, you will see the information message. Calculation cannot be performed if the lattices are different, most likely because of missed lattice type in the text file with specimen data. Move the marker to any specimen line and set the correct lattice.
Calculation will be partially successful if some h k l of the specimen are missed among the standard lines: the texture coefficients for these lines will be empty. For any specimen line, algorithm first tries to find exactly the same indices among the standard. If unsuccessful, it attempts to find the equivalent indices (like 2 1 1 and 1 2 1 in tetragonal lattice). If nothing found, this line will be excluded from calculation because the required intensity is missed. You need to check all such lines and look for better standard or correct the mistakes in the specimen data.
These operations allow to exchange two of the indices h, k, l, or perform the circular shift of the indices to the right or left, or invert the indices h k l where the value k is negative. All actions are performed with the lines of current phase, which is defined by the marker position. When the recalculation is active, you can immediately see the result.
Exchange of two indices can help to change the presentation of lattice, where assigning the parameters to the cell edges sometimes may vary in different sources (the conventional rule is that assigning is determined by the space group). These differences may occur mostly in the orthorhombic and hexagonal lattices. It can also be helpful after indexing.
Circular shift (or rotation) of the indices in the right (h k l → l h k) or left (h k l → k l h) direction may be useful for low-symmetry lattices starting from orthorhombic. It can also be done by two sequential exchange operations, like exchange h and k, exchange h and l for shift to the right.
The purpose of inversion of h k l is to make the indices of triclinic lattice, where negative k is allowed, compatible with monoclinic indices, where k can be only non-negative. This change of presentation may be useful for triclinic structures imported from PDF or AMCSD databases.
Control with keys/mouse: Alt+K or left-click the h k l table header.
You can mark a group of lines as a separate phase with a number from 1 to 4, or define them as the lines of standard substance, or as excluded lines. These lines will have a label instead of their ordinal number: (1) to (4), (s) or " x ". If a phase number is already assigned to the lines, you can restore the ordinal numeration of this group.
If the table already has some phases, only the lines of current phase (defined by current position of marker) will be changed. To assign a label individually to a specific line, use the context phase menu or keyboard command.
This operation can be applied separately to selected and non-selected lines, if they present in the table. In such case, you will see a question, whether to mark all lines or only the selected or unselected ones, depending on current position of marker. Such approach is useful to mark only the calculated or non-calculated lines as another phase.
The common purpose of phase labels is to differentiate the lines belonging to different substances. In particular, you can label the existing lines before adding new lines of other phase to the table using import of *.txt file (all imported lines get the ordinal numbers). Then the difference between them will remain visible after sorting the lines or lattice calculation.
It would be a good idea to write a short note about specified phase in the specimen information.
To remove the specific phase labels and restore the ordinal numeration, set the marker to one of these lines and choose an option "Numbers" (N). To remove all the phase labels in the table, use an option "clear phase labels" in the clear menu.
Here are some advices, which may help to improve the calculation of lattice parameters. They are mostly related to plane specimens, either polished or pressed from powder, with a thin layer of external standard placed on the surface. For other types of specimens, these suggestions may also be helpful because they show the sequence of operations when current step is based on previously calculated data. Anyway, use these advices wisely!
First, you should perform the correction of 2θ by the standard substance. When correction is calculated, you get two parameters of alignment: constant (zero-point) correction and specimen displacement. Constant correction is the most important, while specimen displacement is often approximate because the diffraction area of the specimen is shifted to the depth from the standard substance on the surface. On a properly adjusted goniometer, constant correction should be very small. If it is significant, much more than goniometer precision, consider to check the goniometer adjustment, realign the specimen and repeat the diffractometry.
As for calculated specimen displacement, a small value about a few tenth fractions of millimetre or less can be also found and compensated independently on the last step. Compensation of greater displacement, about 1 mm or more is possible but less reliable, it should be better to realign the specimen and get the diffraction data again.
Calculation of the lattice parameters from initial data allows to evaluate the consistency of data, avoid serious errors and mistakes and get the cell volume with precision enough for next step. Check the details of calculation, look at the root mean square deviation of 2θ (2th rms dev.) and check the outliers (with deviation much more than 3 × precision of 2θ).
At this point, you should try to understand the origin of high deviation of every outlier. It may be a result of simple mistype of a value in the table, wrong line attribution (incorrect indices h k l or a line belongs to another phase), inaccurate separation of the overlapped lines. In the last case it is recommended to repeat the separation using the calculated 2θ (2th calc) of this line as initial position. If there are no such problems or they are solved and calculation results are good, you can go to the next step.
This calculation allows to obtain the molar mass M, density ρ and attenuation length 1/μ; the last is required for 2θ correction depending on the diffraction depth. To perform the calculation of theoretical density, you need to know the number of formula units in the cell, chemical formula of the compound or its atomic composition; you should already know the cell volume from previous step. After calculation, store the initial data and results in a line of specimen information, otherwise you will need to input the formula in this dialog again for new calculation.
Note that calculation of attenuation length in powder and especially in multi-phased specimens is more complex than in single crystalline phase.
Look at the parameter 1/μ: if it is less than about 0.01 mm or if you investigate a layer with thickness much less than 1/μ, the next step may be skipped. Otherwise, you should use this value for more precise angle correction.
With calculated 1/μ, you can return to correction and precision dialog, where all other fields besides this one should be empty. After applying the length, the angles of current phase in the table will be corrected like if all diffraction planes are shifted to the specimen surface, and 2θ become the "true" Bragg angles. Angles of other phases, if they also present, will remain unchanged. After that, it is recommended to perform the calculation of specimen displacement, which can decrease the effect of possible specimen misalignment.
Please remember that this correction, like any other corrections, should be applied only once. Then the field "attenuation length" becomes empty until this value is calculated again.
Calculation of the specimen displacement is the last possible step of improvement of the calculation of lattice parameters. To perform it successfully, you need to check the conditions:
If all conditions are good, perform this calculation and look at the results: the minimal 2θ root mean square deviation, its improvement from current value and the specimen displacement when this minimum is found. For very good alignment, displacement should be very small. For real diffraction data, it may be hundredth or tenth fractions of mm. If the value is much less than attenuation length, this correction may be ignored, otherwise apply it and calculate the parameters last time.
If the displacement is large, like several tenths of mm or more, consider to realign the specimen and perform the diffractometry again.
Two methods of searching the indices are implemented in the program:
Shuffle (permutation) method uses the generated array of h k l, which are sequentially assigned to selected basic lines to get the lattice parameters; a grid of possible reflections is calculated and checked for coincidences until the minimal percent of described lines is reached, then the results are shown in the table. You can set the basic mark "•" on the suitable lines manually (see the recommendations below). If the basic lines are not chosen or number is insufficient, the required lines will be taken from the top of the table.
Limitation: this method does not work for triclinic lattice because it would be inefficient and very time-consuming, even for small h k l. Please use the specialised software or try indexing by known h k l, if they present.
This method assumes that the total number of selected lines with known indices is sufficient to calculate the lattice parameters with quality "satisfactory" or better. Grid of reflections is built from these parameters, then the lines without indices are checked for coincidence. Basic lines are not used in this method, only the limits by h k l, delta and sometimes 2th range should be set. It works with any lattice type.
Such method may be useful when some indices, usually belonging to a few first or strongest lines, should be the same as in a structure prototype, but the differences in lattice parameters make hard to attribute the lines at larger 2θ angles directly.
Two described methods can work in sequence: if you have a lot of lines of the substance with low-symmetric lattice, which the shuffle method is not able to process for reasonable time or because of internal overflow, you can perform the indexing of less number of first lines with lower limits by h k l, select the best result and then identify the rest of lines using the second method.
For the shuffle method, good choice of basic lines may greatly affect the success of indexing. Their number should be equal to the number of lattice parameters, e.g. one for cubic, two for hexagonal, tetragonal and rhombohedral lattice etc. Lines are counted from the top of the table, so if the number of lines marked as basic is not enough for current lattice, additional lines will be taken from the top; if too many lines are marked, the extra lines will be ignored.
Selecting the best basic lines may require several attempts of trial and error. First, note that the default selection of basic lines from the top of the table is usually not the best: the exact lattice parameters calculated from the lines with smaller 2θ may have significant errors, preventing the attribution of the lines with larger 2θ. It would be more reasonable to select the lines in the middle or even near to the end of 2θ range. On the other side, take into account the intensities: the more intensive non-overlapped lines usually are more reliable. You may sort the lines by descending of intensities and choose the basic lines from the top of the table. Usually, 2θ angles of the most intensive lines are defined more precisely than others. However, it may not guarantee that these lines are independent. Try to mark different lines (most intensive and with large 2θ) until you get the suitable results.
Sometimes a wrong selection may be hard to predict, for example, if you occasionally chose the lines which are linearly dependent or do not include one axis (like h k 0 in tetragonal lattice). In this case, you may get poor results or no results at all. Changing one basic line to another one may resolve such issue.
In a shuffle cycle, the basic lines get the current combination of indices from generated h k l array, indices in the array are sorted by increasing of sum of squares; the repetitions in cubic, rhombohedral, hexagonal and tetragonal lattices are skipped. Then the lattice parameters are calculated from basic lines and checked against given limits by a b c and V. A grid of possible reflection angles is built from the h k l array and is used to search for the reflections adjacent to experimental angles within the delta × precision interval. Indices of reflections may be checked for cell centring with higher symmetry (which is limited by higher possible centring of basic lines). If the percent of adjacent lines is high enough, their indices are used to calculate the lattice parameters more precisely, and the results are shown in the table and in the dialog with the result of current cycle (in the interactive mode).
Every successful cycle is checked for cell volume and number of described lines; if one of both of them are better than obtained in previous cycles, they are memorised to be shown in the dialog with the results of indexing when all cycles are completed.
This dialog allows to input the parameters which define the indexing process. Before using this dialog, you need to set the supposed lattice type.
For the shuffle method, it is highly recommended to choose the basic lines (use the phase menu or "B" key, also see advices in the previous section).
For the method by known h k l, it is suggested to calculate the lattice parameters by known lines and, if the number of selected lines is more than number of lattice parameters, check that quality is "satisfactory" or better. This method uses only the limits by h k l, delta and 2th range when need.
Limits by h k l: 5 5 5
The higher limits increase the chance of success, even with non-minimal cell, but increase the total number of cycles and calculation time. A size of h k l array in Win32 version of the program is 4096. For a primitive cell and for cubic lattice h k l must not exceed (46 46 46) with multiplicities, for orthorhombic lattice — (15 15 15) and for monoclinic one — (12 12 12). If a cell is non-primitive, limits can be increased.
For indexing by shuffle of monoclinic lattice, the limits more than (4 4 4) may be very time consuming and inefficient. Try to set the limits when the array size (shown in the information line) would be around 100...200. You can decrease 2th range and then use less limits by h k l to try to identify some (like 10...15) first lines. Indexing by known h k l, on the other hand, is performed without multiple cycles and is quite fast, hence use the limitations from previous paragraph.
If you input less than 3 values in this one and next fields (for any lattice), missed values will be copied from the last input value. For indexing by known h k l, if some values are less than the maximal indices in the table, program shows the warning and asks whether you want to Increase the limits, which are less than in the table, or Continue without changes.
Limits by a b c: 10 10 10 (length in Å) or 1 1 1 (length in nm)
Set a maximum size of cell in 3 dimensions. Higher values increase a chance to find the non-minimal cells, while too low values will make the correct indexing completely impossible. Always check that these values are not less than in a prototype cell. Possible limits 2...99 Å or 0.2...9.9 nm.
If you do not have a prototype, use this approach: they should be no less than the maximal sum of d and ±d × delta. For hexagonal lattice type, need to multiply d by 2/√3. If supposed cell symmetry is high, need to take into account the possible extinctions. For example, third index in HCP lattice starts from two: (0 0 2), so the limit should be no less than max of 2 × (d + 4 × ±d), if the delta multiplier is 4.0.
Limit by beta: 125
This setting is available only for monoclinic lattice. Beta angles beyond 110...120 degree may exist, but are quite rare; proper limitation reduces the time of calculation. Like for cell edges, too low value will prevent from getting the correct results. Possible limits 90...150.
Limit by V: (cell volume in Å3 or nm3)
Volume limitation can decrease the number of non-minimal found cells, especially when the limits by a b c are high. This field is empty by default and is not used. If you decide to set this limit, it would be reasonable to use the volumes obtained in previous calculations as a reference point.
If the limits by a b c were increased in this dialog but the limit by V was not, the program shows a request if old volume becomes a limitation. You can continue indexing or cancel it and either change the limit manually or clear this field.
Threshold, %: 80
Minimal percent of described lines. Recommended value 70...90, possible limits 25...100.
Delta multiplier: 4.0
This value is a multiplier of 2θ precision, which defines an interval of 2θ for search for adjacent reflections. In some cases a value from 3 to 5 may be reasonable: 3.0 is a strict limit when all lines should be within the interval of satisfactory quality, may be useful for indexing by known h k l; 5.0 is a less restrictive limit to find the lines in more wide area, may be useful for shuffle. Possible limits 1.0...10.0.
Generally, if you have the problems with indexing, try to set the more appropriate 2θ precision before changing this parameter.
2th range: 0 180
Normally the angle limits for indexing are taken automatically from the unidentified lines with lowest and highest 2θ with adding delta × precision on both sides. The setting here creates the additional limitations which may help in the case of error too many h k l combinations. Selecting a more narrow range of angles may greatly reduce the number of possible combinations, especially for low-symmetric lattices.
For the shuffle method, this setting allows to select only a part of existing lines, if their number is too big. Decreasing the upper limit may be enough: the lines with lower 2θ may be identified with lower limits by h k l. After that, the remained lines can be described using the method by known h k l without 2θ restriction.
Besides these cases, it is recommended to keep the default non-restrictive values; to restore them, clear this field.
Interactive search mode
Selecting this check box allows to perform the indexing by shuffle in interactive mode, when the dialogs with intermediate results are shown after every successful cycle. This can be useful if you want to see some possibly interesting results, which were not shown after performing the non-interactive search because they did not meet the best search criteria (minimal cell volume or maximum of described lines). When the check box is clear, all intermediate dialogs are skipped and the results of indexing are shown when all cycles are completed.
When initial settings are ready, press Start to begin the indexing process by shuffle (for a lattice from cubic to monoclinic) or by the lattice parameters which are calculated from the lines with known indices.
Alt+I - dialog of indexing by shuffle Alt+B - dialog of indexing by known h k l Alt+R - results of indexing after finish Esc - interrupt indexing cycles (may take some time)
On the bottom line of the screen, you can see current information about indexing cycle: size of h k l array, number of successful cycles and current indices assigned to first basic lines (for orthorhombic or monoclinic lattice). The cycles by h k l are going on in ascending of the sums of their squares. If the parameters calculated for basic lines are within the limitations defined in the indexing settings and the percent of lines, which are located near theoretical positions calculated from these parameters, is high enough, the cycle is counted successful. The described lines are marked by bluish background in the table, and calculated lattice parameters are shown on the screen.
If the search is being performed in non-interactive mode, you can interrupt it (use the "Esc" key or toolbar button "Results") and either change the indices of the first basic line to next combination (to skip the rest of shuffle with current indices) or exit the cycle and see the obtained results.
You can interrupt the indexing process by pressing the "Esc" key or toolbar button "Results". Attempt to perform any other operation shows the warning that chosen operation will stop the indexing. If you confirm that by OK, indexing will be stopped and current data in the table used for operation. Cancel will continue the indexing. Some operations like editing the table, changing the wavelength or lattice type are not available during indexing.
Interrupt is possible only for low-symmetric lattices, indexing of lattices with high symmetry is usually fast enough. Interrupt may not happen immediately, it may take some time.
After interrupting, the dialog shows the number of successful cycles and possible options. You can Continue the indexing in normal way, or change the indices of the first basic line to the Next h k l combination, or Stop the cycles and show the dialog with the results of indexing.
Next combination may be useful to quickly skip current h k l if some of the indices are high and unlikely may give more results, so better to begin the next cycle with initial low indices. Before choosing to stop, take into account that the intermediate results may be greatly incomplete. Use stop if you want to change some settings or correct other mistakes, or if the indexing process with current settings takes too long time.
When the interrupt is a result of attempt to close the program, the options in this dialog change. Instead of the next combination, you can Close the program immediately. Warning: all progress of the indexing will be lost.
This dialog shows the result of current indexing cycle: the number of described lines and cell volume; you can see current lattice parameters in the table (move the dialog if need). You can Continue the indexing in normal way or change the indices of the first basic line to the Next h k l combination.
You can also Stop the indexing, if you want to change the initial settings or check the current results more carefully. In the last case, press Cancel in the next dialog, then you can save or print the table.
When indexing is finished, the operation "Results" shows the dialog with the results of indexing until the original data in the table are the same: lines are not changed, 2θ correction or specimen displacement is not applied.
You can select or unselect the lines, sort the lines, calculate lattice parameters and see the details, calculate specimen displacement but not apply it. Any operations which change data in the table will clear the results. To keep the results, save current table and work with a copy.
Remark: if you select or unselect the lines (manually or in the details of calculation dialog), the percent of described lines will no longer be available. Use the dialog "Results" to restore the original selection and this percent.
Indexing is finished, when the indices of first basic line reach the maximum h k l values, then the program shows the dialog with found results. Two criteria of selection are used: by minimal cell volume and by maximum of described (identified) lines. If several results with the same volume are found, the first is taken because the indices h k l are minimal at the start of shuffle; if several results with the same number of lines are obtained, the result with minimal volume is used. If both the number of lines and volume are the same, the result with higher cell centring will be taken.
You can choose which result, Min volume or Max lines you would like to see in the table, or cancel to keep the last successful result. Besides these choices, pay attention to the results where the cell is more symmetric (if a structure prototype may have a non-primitive cell) and where the indices of basic lines are relatively small. If need, you can repeat the indexing with different basic lines, different cell centring and compare the minimal volume and percent of described lines.
To choose other result, use "Results" in the menu "Calculate" or the corresponding toolbar button. This dialog will be available until the data in the table are not changed manually or by applying any correction. If you find both results valuable, save each of them to separate file before changing the lines.
If the initial settings were unsuitable (incorrect basic lines were selected, threshold is too high, limits by h k l or lattice constants are too small, incorrect lattice type or cell were chosen), the results will be probably unreliable. You may also see the message like "Failed in finding any indices". Try to change some initial indexing settings and repeat the process.
The results of indexing are shown immediately because all operations are performed in a single cycle. If successful, the unidentified lines get the possible indices but remain not selected (white or yellow with the marker). This separates them from selected lines, which were used to calculate the initial lattice parameters. If you want to improve the lattice parameters by adding the newly described lines, select some of them manually or all by command Ctrl+A and perform the calculation.
If more than one possible h k l combination was found for a line within delta × precision interval, the program creates the copies of this line with all found combinations and shows them as a group with the same 2θ angle. You can choose the lines in the group by some criteria: minimal 2θ deviation (most common), indices h k l belong to a more symmetric cell, specific h k l combination presents in a structure prototype. To improve the calculation of parameters in such case, select only one suitable line in each group; you may either not select or delete other lines.
The most common cause of unsuccessful indexing is too large deviation of unidentified lines from the calculated position — more than delta × precision. You can either change the delta multiplier or, better, set the more appropriate 2θ precision in the correction and precision dialog.
Also, try to re-assign one or more basic lines to avoid a problem with too large deviation of chosen lines or unlucky choice of dependent indices; slightly decrease the threshold. Besides that, try to increase the limits by h k l and edges, set the primitive cell and change the lattice type to another possible.
This is a simple example of indexing by shuffle of the diffractometry data, imported from the program Match! (powder of α-Zr alloy with hexagonal lattice, emission Cu Kβ). List of 2θ and I of this specimen is shown in the text files section, second example.
First, you need to set the emission Cu Kβ and ångströms unit, select hexagonal lattice, then copy the diffraction data to clipboard (click the list) and paste it to the table (Ctrl+V) as d value. Check 2θ precision: this is an important step. For this example, the default value 0.01 degree is suitable, but 0.02 is more correct by the conditions of diffractometry. Input it in the correction and precision dialog (Alt+E), "Set 2th precision".
Next, need to define the basic lines: two for hexagonal lattice. In this particular example you can skip this step; the program will mark the required number of lines from the top of the table automatically. However, you can set the basic marks manually (B), e.g. by choosing two most intensive lines.
Before start of the indexing, need to input initial settings (Alt+I). For this example, the default limits by h k l (5 5 5) and a b c (10 10 10) are suitable: lattice parameters of Zr are less than 10 Å, expected indices at existing angles are relatively small. Otherwise, change these settings accordingly. Other default settings should not be changed without reason.
Now Start the indexing: for such high-symmetry lattice it completes very quickly. Check the results: in this case, two criteria (minimal volume and maximum lines) are the same, 100% of lines are successfully indexed. Choose Min volume to see the results in the table and calculated parameters.
Although 2th rms dev is smaller than precision and result of lattice calculation is counted excellent, it still can be improved. Check the details of calculation (Alt+D): the mean deviation is noticeably shifted from zero, which may be a result of specimen displacement. You can find this (Alt+P), but note that recall of the results of indexing will no longer be available. Graph on the dialog shows that the shift is about -0.12 mm (for the default radius of detector circle 200 mm). You can apply this value and get the corrected lattice parameters with smaller divergence.
File or directory is not found, cannot be opened or is write-protected. More likely, you made a mistake typing the name. Another possible reason: you deleted of moved to another place a file, which was stored in the recent list; this file will be removed from the list and you need to find it using open the table dialog. Less often, you may see this error when you do not have an access to external drive or lack of required permissions. If the file is write-protected and cannot be saved with the same name or in the same place, try to change its name or use another directory or drive in save as dialog.
You have chosen the name of the file, which already exists. If you want to rewrite it, confirm it in the dialog, otherwise cancel and try to choose another name. Alternatively, you can change a directory or drive and save the file there.
You try to open a file with the size more than 64 Kbytes, most likely by mistake. You still can open it, but any lines after this limit will not be input to the table. Common data files supported by the program should not exceed this limit, if they have no more than 440 diffraction lines. Attempt to input more lines will result in the table size overflow error.
Open this file in a text editor such as Notepad and check its format. If the file has too many data lines, try to split it to two or more; do not forget to keep the file header with diffractometry information.
This dialog shows several first lines of a file or clipboard, which the program was not able to recognise. It may happen because of incorrect data in a source or if the format is not supported by current version of the program.
If you open a file, check that it has one of supported formats: *.htm, *.par, *.aid or *.txt, they are described in the open the table section. Note that although the files *.par and *.htm use the common text format, changing any data is recommended only in the program interface. If you open such file in external editor to copy results to a report or publication, try to choose the read-only mode or at least do not save any change.
Generally, format of clipboard data should be the same as of files. If the lines copied to clipboard were selected incorrectly, Cancel and try to copy the lines again. If the data are not recognised because of a few wrong symbols, press Clipboard to open the clipboard content dialog and correct the lines manually by deleting or changing some text. After correction, you can paste the data in that dialog. Please note, when you select a block of text in external source, pay attention to the begin of the block, which should start from the first symbol in a line. Otherwise, this line (or the whole block) may be input incorrectly.
List of diffraction lines in text format, which contain 2θ or d and may include intensities and h k l, should not have other data (except of commented lines started from ";"). All values are checked for acceptable limits, e.g. 2θ or d should be greater than zero, 2θ should be less than 179 etc. Incorrect values will not be accepted or they may stop the data input after a wrong line.
This file does not contain the information about the wavelength. Most often, this may happen when the wavelength is missed in the header of the imported text file. However, some PDF files may also omit this information (such cards are incomplete and eventually become marked as deleted).
Current wavelength is not changed: it was used to calculate 2θ or d, depending on primary data in the file. You can choose another wavelength, which corresponds to original data, and recalculate them. If the precision has been calculated, it is recommended to reopen the file after changing the wavelength. For the data from external sources, the most common emission Cu Kα1 (1.54056 in PDF) may be a reasonable choice. If you imported the interplanar distances or PDF data, then selecting the approximately similar emission is enough, because in such cases the exact value of wavelength does not affect the calculation of parameters.
This message means that a file does not contain an information about lattice type of the substance. This may happen, for example, if you opened a very old PDF card. Primitive cubic type is assigned by default to this lattice. As a result, an attempt to calculate the lattice parameters may give wrong results.
You need to select the real lattice type if it is known. Otherwise, try to assign the probable types which can be concluded from existing h k l combinations, then perform the calculation and see how many errors (very large deviations) are in the results. Alternatively, you can try to use the indexing procedure.
The minimal number of the lines with linearly-independent indices, which are selected for calculation, must not be less than number of lattice parameters in given syngony; for statistical reliability this number should be more than minimal. Try to select more lines or add them to the table.
Indexing requires at least one extra line over the number of lattice parameters. Besides that, for indexing by known h k l the number of known and selected lines should be enough to calculate the parameters.
Most of PDF-2 cards, including the theoretically calculated data, have at least 5 digits after the decimal sign in the d values, so the default precision, which is defined in the options, is applied to these data. However, some old cards (circa 1950-1980) may have only 3 or 4 significant digits (the rest of digits required by the card format are zeroes). If this occurs, the program restores the approximate 2θ precision basing on the number of significant digits of d and current wavelength; in such case, the default precision is not used. The calculated value is normalised to the nearest value in the standard precision row. If need, you can set 2θ precision manually in the correction and precision dialog.
There may be a number of reasons to change current wavelength when the table contains some data. You might read (import) a file without information about wavelength, or you want to see 2θ at different emission than in imported card or your previous calculation. You might also skip to set the correct wavelength before input data in the table manually.
In this dialog, you need to choose how to recalculate the existing data. If the angles 2θ are original, like the data from XRD device, need to calculate new d from 2th; otherwise, if the d values should be counted original, like in PDF cards, need to calculate new 2th from d. You may also Cancel the change and return to previous wavelength.
Changing the wavelength may require to calculate new 2θ precisions. If the angles are original, precisions remain unchanged. They also remain the same if the d values are original, but all lines have the same 2θ precision equal to default PDF precision in options or the last set 2θ precision in the correction and precision dialog. Otherwise, the precisions are calculated separately for each line from d and its current precision. As a result, even in the constant mode they may be different.
In any case, if the new precisions calculated this way are not correct, you can change them in the correction and precision dialog.
This warning means that wavelength of the added or pasted lines is different from current wavelength. This may happen when you have some data in the table and open another file with different wavelength or paste the copied lines from clipboard. It may also happen when the lines copied to clipboard are pasted in different program session with different wavelength.
For the lines from clipboard, which do not have specified wavelength, program checks the data consistency by reconstructing the mean wavelength and comparing it to current. For the lines from opened file, wavelengths are compared directly. If new wavelength is close to current (within relative difference 0.00067, see select the emission), they are counted the same. If the difference is significant, you need to decide:
Both choices may have some disadvantages.
If you calculate new 2θ from d, some of added lines may be lost because of non-reflecting d. Moreover, precision of 2θ will be recalculated from precision of d and may become different from original diffractometry.
If you decide to change current wavelength, for the clipboard lines the program will try to find the closest emission from the list. If not success, the calculated wavelength will be used. Also, as in the previous case, some 2θ of current lines may be lost and precision may change too.
You can also Cancel the addition and then decide how to convert the data to the same wavelength with minimal loss of quality.
The number of lines with linearly-independent indices is less than minimal number required for calculation, which is equal to the number of lattice parameters. More often, this may happen at calculation of low-symmetric lattices, especially when the total number of lines is low or when you attempt to unselect too many lines with high deviation. Another cause may be lack of the lines with specific indices, for example, lines with non-zero k for orthorhombic lattice.
Try to select more lines for calculation or choose some other lines instead.
This error may happen if you attempt to generate reflections by parameters, but you have selected very narrow 2θ range or the upper 2θ limit is too low. You might also set unusually large wavelength. Try to increase 2θ range until the error disappears.
This error means that the number of h k l combinations generated for the limit by indices in the Settings for indexing dialog is not enough to continue the indexing process. This number should not be less than the number of lattice parameters plus one. Return to the indexing dialog and increase some of h k l limits.
This error message usually happens at the start of indexing, but may also happen if you try to generate the reflections of the large cell in large 2θ range. It informs about the overflow of the array of possible h k l combinations, which is limited by 4096 in current Win32 version of the program.
In the indexing mode, if a cell centring is primitive, use these estimations: h k l must not exceed (46 46 46) (with multiplicities) for cubic lattice, (15 15 15) for orthorhombic, (12 12 12) for monoclinic, (9 9 9) for triclinic. If a cell is non-primitive, limits can be increased. For shuffle method, decrease one or more maximum values by h, k or l, until the overflow disappears. For the indexing by known h k l method, you can keep recommended indices but instead decrease the 2θ range, selecting the more narrow area around the unidentified lines.
In the generation mode, this may happen if the edges are large and the 2θ range is very large as well. For example, for cubic lattice, Cu Kα emission and 2θ range 0...179 degrees the maximum edge a is 53 Å. However, the table becomes full at much lesser 2θ range 0...40 degrees. For tetragonal lattice, the edge limits are approximately 20 Å, for orthorhombic — 15 Å, for monoclinic — 12 Å, for triclinic — 9.5 Å. To prevent this kind of overflow, use a reasonable upper 2θ limit or decrease it until this error disappears. You may still see the warning about the table size overflow, but the program will automatically decrease the upper 2θ to acceptable value.
This error may happen in different cases: when loading data from a file, when generating the table of reflections, or at the end of indexing. It means that table size has reached the maximum limit (440 lines).
When loading data to empty table, this should happen extremely rare (supposedly, only for some AMCSD files). But it may occur when you try to add the data to existing table by import from a file, or paste too many lines from clipboard. In such cases, you can clear the table, or remove some less important phases from the table, or remove extra lines from the source file, or copy less data to clipboard and repeat the operation.
When you perform the generation reflections by parameters, if the number of possible h k l combinations for given 2θ range exceeds the table size, the program automatically decreases the upper 2θ limit. As a result, all possible reflections beyond the limit are missed. See the last calculated angle at the end of the table and use it as a reference point for another 2θ range.
This error may also happen after indexing by known h k l. Normally any line with several h k l combinations found within the delta area around 2θ is shown in the table multiple times. When the added lines reach the table size, indices of the lines after that point remain partially or completely unknown. It is recommended to save current results, then delete the identified lines using the clear non-selected lines operation (except the last one: keep a single line with 2θ and clear its indices). Then perform the indexing of remained lines again.
Indexing by known h k l begins from calculation of lattice parameters by selected lines with known indices. The quality of calculation directly affects the success of indexing; because of this, the quality should be at least "satisfactory" or better. "Poor" quality means that root mean square deviation is more than 3 × precision, so indexing cannot continue.
First, check if the lattice type is correct and the precision is real. Then perform the calculation of lattice parameters and look at the recommendation in details. Try to unselect the lines with too high deviation and select other lines until you get the "satisfactory" quality or better if possible. As a last resort, you can select the minimal set of lines equal to the number of lattice parameters, when estimation of quality is not performed.
To perform indexing by known h k l, the lines, which indices you want to identify, should have the empty h k l field and belong to the same phase as known lines, if the phase is specified. Unselected lines with non-zero indices and 2θ angles are counted as known. Please make sure that unidentified lines present in the table; also if the table has more than one phase, move the marker to any line of specified phase.
The lattice parameters have been calculated by the lines with known indices h k l, but an attempt to find the indices of any unidentified line was failed. A probable reason is, the real precision of 2θ angles is significantly poorer than the precision, which is currently set for these lines. Try to change the 2θ precision to value that is more correct. Otherwise, these lines may belong to another phase with different crystal structure or less symmetric cell.
This message means that calculated results do not have a physical sense, e.g. negative lattice parameters were obtained. More probably, this may happen because of some mistakes like wrong indices or angles, for example, when the same indices are assigned to significantly distant lines.
Thoroughly check all data in the table. Also, try to select more lines, if possible, then unselect one or several lines until this error disappears. These unselected lines may have significant deviation, often far beyond the mean value.
Other causes of this error may be a wrong lattice type or too few linearly-independent indices. Check and try to change the lattice type, add more lines for calculation.
Chemical formulae, which are input in the theoretical density dialog, may contain some errors preventing the proper decryption of the formula and, as a result, the calculation of molar mass and density cannot be performed. In such case, you will see one of error messages in the line for atomic composition. Sometimes the decryption algorithm may show errors for valid but too complex formula: please send an example of such formula with explanation to author for test. Note that algorithm was not designed for complex organic compounds and polymers.
This error means that you made a mistake in a symbol of one of chemical elements. Program can recognise only the standard short names of 1 or 2 letters; other non-standard, temporary, obsolete variants or abbreviations like Tu, Yt, Ln, Me etc. are not accepted. Some such names may be mistakenly interpreted as two existing elements. This error may also happen when the letter case is incorrect (decryption algorithm can correct some mistakes, but not all). Check the formula and look at the official symbols of elements in the up-to-date periodic table, for example, in the PubChem database [7].
Only the limited number of signs and punctuation marks may be used in a formula: spaces, tabulation, semicolon, plus, round and square brackets, decimal dot (period) and centre dot signs; other signs are not currently supported. Check the formula and delete or replace a wrong character. Be careful when pasting a formula from HTML (web page) or PDF publication: it may contain some internal formatting characters, which result in this error. In such case, delete all non-formula characters, including those, which are visible like spaces.
Such error may happen if the number of closing brackets is not equal to opening brackets, if the closing bracket presents before opening or if the different types of brackets are used as opening and closing on the same level. In any such situation, the coefficient after closing bracket cannot be properly applied. Check that all brackets are correct and paired.
Number of formula units in the cell should be integer; currently supported values are within the limits 1...128. Note that the field "Units" should be empty (or have 0) to calculate the number from the density stored in AMCSD file. In other cases, only the molar mass M will be calculated.
Formula may have up to 16 different types of atoms (common chemical elements and specific isotopes), otherwise it cannot be decrypted because of complexity. If you work with the compounds like multi-component high-entropy alloys, try to combine some less important or similar (by atomic mass) elements.
Total number of atoms of particular type is more than maximum possible, currently 2000. This error may occur because of too large coefficient or common multiplier in the formula. Check these values.
Coefficient or multiplier is most likely too small, too large or contains non-translatable characters. This value should be from 0.00001 (1E-5) to 2000. Check the value and avoid to use the extended Unicode characters. Note that arithmetic operations like 2-0.15 are not allowed here. Values should be calculated before using in a formula.
Most likely, the algorithm has recognised a part of the formula as two consequent coefficients, which is not allowed. Remove the second value or add the missed element or brackets. If this is a multiplier written before a group, like a coefficient of hydration, use one of possible separators: * (asterisk) or · (middle dot) or ⋅ (dot operator) or • (bullet).
If you specified the atomic mass of an isotope in the brackets after the element name, check that the value is within the limits 1...330 (g/mol), according to possible masses in current periodic table.
Formula line is empty or cannot be interpreted as a chemical formula: no elements are found. Please note that this dialog cannot be used to input or edit any specimen information besides the formula; if you need this, use the information about specimen dialog instead.
Such error occurs if there is a comma inside the brackets, which means that some elements are mixed or exchanged in unspecified proportion, like olivine (Mg,Fe)2SiO4. Without definite information of elements quantity, the molar mass and density cannot be calculated. This can be solved in two different ways. First, you can specify the amount of each element in the compound, like (Mg0.6Fe0.4)2SiO4. Second, you can calculate the density for each variable element separately. Then, depending on the purpose of research, you can describe the possible interval of the density or calculate the mean value and uncertainty.
There is an internal limitation of formula complexity: it may have no more than 4 levels of nested brackets, including round and square brackets and also brackets of isotopes; nesting of the square brackets is not supported. Try to rewrite and simplify the formula if possible. Alternatively, instead of the formula you can write the list of atoms and their amount in the unit, as it is shown in the decrypted atomic composition.